题目内容
【题目】(1)问题发现
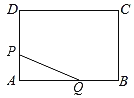
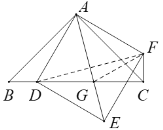
如图①,![]() 是等腰直角三角形,四边形
是等腰直角三角形,四边形![]() 是正方形,点
是正方形,点![]() 与点
与点![]() 重合,则线段
重合,则线段![]() 与
与![]() 之间的数量关系和位置关系分别是 .
之间的数量关系和位置关系分别是 .
(2)深入探究
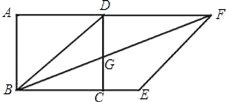
如图②,![]() 是等腰直角三角形,四边形
是等腰直角三角形,四边形![]() 是正方形,点
是正方形,点![]() 在直线
在直线![]() 上,对角线
上,对角线![]() 所在的直线交直线
所在的直线交直线![]() 于点
于点![]() ,则线段
,则线段![]() 之间有什么数量关系?请仅就图②给出证明.
之间有什么数量关系?请仅就图②给出证明.
(3)拓展思维
如图②,若点![]() 在直线
在直线![]() 上,且线段
上,且线段![]() ,当
,当![]() 时,直接写出此时正方形
时,直接写出此时正方形![]() 的面积.
的面积.

【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)5或13
,证明见解析;(3)5或13
【解析】
(1)根据已知可得CF⊥BC,AD⊥BC,即可得出BD⊥CF,再根据等腰三角形的性质即可得出BD=CF;
(2)连接DF,GF,先证明△BAD≌△CAF,再根据勾股定理即可证明;
(3)分①当D在BC上时和②当D在BC的延长线上时,两种情况结合正方形的性质及勾股定理进行讨论求解即可.
解:(1)BD=CF,BD⊥CF
∵ADEF是正方形,
∴∠ADE=∠FCD=90°,AD=CD=CF=AF,
∴CF⊥BC,AD⊥BC,
∴BD⊥CF,
∵△ABC是等腰直角三角形,AD⊥BC,
∴D是BC中点,
∴BD=CD,
∴BD=CF;
(2)BD2+CG2=DG2,
证明:连接DF,GF,
∵四边形ADEF是正方形,
∴AE垂直平分DF,AD=AF,∠DAF=90°,
∴DG=FG,
∵△ABC是等腰直角三角形,
∴AB=AC,∠BAC=90°,∠B=∠ACB=45°,
∴∠BAC-∠DAC=∠DAF-∠DAC,
即∠BAD=∠CAF,
在△BAD和△CAF中,
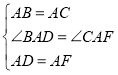 ,
,
∴△BAD≌△CAF(SAS),
∴BD=CF,∠B=∠ACF=45°,
∴∠GCF=∠ACB+∠ACF=90°,
在Rt△GCF中,由勾股定理,得CF2+CG2=FG2,
∴BD2+CG2=DG2;
(3)①当D在BC上时,
如图,过A点作AH⊥BC于点H,
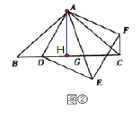
∵△ABC是等腰直角三角形,
∴AH=BH=![]() BC=2,
BC=2,
∵BD=1,
∴DH=BH-BD=1,
∴在Rt△ADH中,AD=![]() =
=![]() ,
,
∴S正方形ADEF=AD2=5;
②当D在BC的延长线上时,
如图,过A点作AH⊥BC于点H,
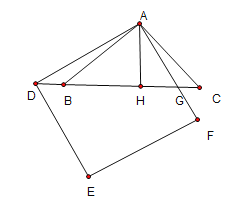
∵△ABC是等腰直角三角形,
∴AH=BH=![]() BC=2,
BC=2,
∵BD=1,
∴DH=BH+BD=3,
∴在Rt△ADH中,AD=![]() =
=![]() ,
,
∴S正方形ADEF=AD2=13;
综上:正方形ADEF的面积为5或13.

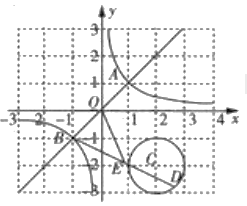
【题目】如图,反比例函数![]() 与正比例函数
与正比例函数![]() 交于格点(网格线的交点)
交于格点(网格线的交点)![]() .
.
(1)填空:![]() ;
;![]() ;
;
(2)当![]() 时,直接写出
时,直接写出![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)点![]() 是以格点
是以格点![]() 为圆心,
为圆心, ![]() 为半径的圆上一动点,连接
为半径的圆上一动点,连接![]() 取
取![]() 的中点
的中点![]() 试确定线段
试确定线段![]() 的取值范围.
的取值范围.
【题目】![]() 三位女同学竞选学校即将组织的“中国梦,我的梦”文艺演出女主持人,它们的笔试成绩和口试成绩、形象得分,分别如下:
三位女同学竞选学校即将组织的“中国梦,我的梦”文艺演出女主持人,它们的笔试成绩和口试成绩、形象得分,分别如下:
|
|
| |
笔试 |
|
|
|
口试 |
|
|
|
形象 |
|
|
|
平均分 |
|
|
|
(1)①![]() ;
;
②在表格中的![]() 个数的中位数是 ,众数是
个数的中位数是 ,众数是
(2)经学校研究决定,在![]() 两位同学中选一位.评比方法:按笔试成绩:口试成绩:形象得分
两位同学中选一位.评比方法:按笔试成绩:口试成绩:形象得分![]() 进行计算,得分最高的同学为本次文艺演出的女主持人.请你算一算哪位同学最后被选为本次文艺演出的女主持人?
进行计算,得分最高的同学为本次文艺演出的女主持人.请你算一算哪位同学最后被选为本次文艺演出的女主持人?