题目内容
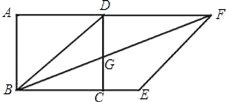
【题目】如图,△ABC中,![]() ,
,![]() 于点D,
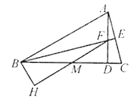
于点D,![]() 于点E,交AD于点F,点M是BC的中点,连接FM并延长交AB的垂线BH于点H.下列说法中错误的是( )
于点E,交AD于点F,点M是BC的中点,连接FM并延长交AB的垂线BH于点H.下列说法中错误的是( )
A.若![]() ,则
,则![]()
B.若![]() ,则
,则![]()
C.若![]() (点M与点D重合),则
(点M与点D重合),则![]()
D.若![]() (点B与点D重合),则
(点B与点D重合),则![]()
【答案】D
【解析】
连接CF,由垂心的性质得出CF⊥AB,证出CF∥BH,由平行线的性质得出∠CBH=∠BCF,证明△BMH≌△CMF得出BH=CF,由线段垂直平分线的性质得出AF=CF,得出BH=AF,AD=DF+AF=DF+BH,由直角三角形的性质得出AD=![]() BD,即可得出结论;同A可证:AD=DF+AF=DF+BH,再由等腰直角三角形的性质和含30°角的直角三角形的性质即可得出结论.
BD,即可得出结论;同A可证:AD=DF+AF=DF+BH,再由等腰直角三角形的性质和含30°角的直角三角形的性质即可得出结论.
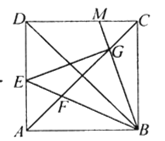
解:连接CF,如图所示:
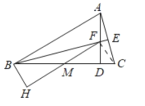
∵AD⊥BC,BE⊥AC,
∴CF⊥AB,
∵BH⊥AB,
∴CF∥BH,
∴∠CBH=∠BCF,
∵点M是BC的中点,
∴BM=MC,
在△BMH和△CMF中,
∠MBH=∠MCF,BM=MC,∠BMH=∠CMF,
∴△BMH≌△CMF(ASA),
∴BH=CF,
∵AB=BC,BE⊥AC,
∴BE垂直平分AC,
∴AF=CF,
∴BH=AF,
∴AD=DF+AF=DF+BH,
∵在Rt△ADB中,∠ABC=30°,
∴AD=![]() BD,
BD,
∴DF+BH=![]() BD,故A正确;
BD,故A正确;
同A可证:AD=DF+AF=DF+BH,
∵在Rt△ADB中,∠ABC=45°,
∴AD=BD,
∴DF+BH=BD,故B正确;
同A可证:AD=DF+AF=DF+BH,
∵在Rt△ADB中,∠ABC=60°,
∴AD=![]() BD,
BD,
∴DF+BH=![]() BD,故C正确.
BD,故C正确.
故选:D.

 小学课时特训系列答案
小学课时特训系列答案【题目】![]() 三位女同学竞选学校即将组织的“中国梦,我的梦”文艺演出女主持人,它们的笔试成绩和口试成绩、形象得分,分别如下:
三位女同学竞选学校即将组织的“中国梦,我的梦”文艺演出女主持人,它们的笔试成绩和口试成绩、形象得分,分别如下:
|
|
| |
笔试 |
|
|
|
口试 |
|
|
|
形象 |
|
|
|
平均分 |
|
|
|
(1)①![]() ;
;
②在表格中的![]() 个数的中位数是 ,众数是
个数的中位数是 ,众数是
(2)经学校研究决定,在![]() 两位同学中选一位.评比方法:按笔试成绩:口试成绩:形象得分
两位同学中选一位.评比方法:按笔试成绩:口试成绩:形象得分![]() 进行计算,得分最高的同学为本次文艺演出的女主持人.请你算一算哪位同学最后被选为本次文艺演出的女主持人?
进行计算,得分最高的同学为本次文艺演出的女主持人.请你算一算哪位同学最后被选为本次文艺演出的女主持人?