ћвƒњƒЏ»Ё
°Њћвƒњ°њƒ≥–£ќ™ЅЋљв—І…ъЅг”√«Ѓ÷І≥ц«йњц£ђі”∆я°Ґ∞Ћ°ҐЊ≈ƒкЉґ800√ы—І…ъ÷–Ћжїъ≥й»°≤њЈ÷—І…ъ£ђґ‘Ћы√«љсƒк5‘¬ЈЁµƒЅг”√«Ѓ÷І≥ц«йњцљш––µч≤йЌ≥Љ∆£ђ≤Ґїж÷∆≥…»зѕ¬Ќ≥Љ∆ЌЉ±н£Ї
„й±р | Ѕг”√«Ѓ÷І≥цx£®µ•ќї£Ї‘™£© | ∆µ э£®»Ћ э£© | ∆µ¬ | |
љЏЉу–Ќ | “ї | x£Љ20 | m | 0.05 |
ґю | 20°№x£Љ30 | 4 | a | |
Єї„г–Ќ | »э | 30°№x£Љ40 | n | 0.45 |
Ћƒ | 40°№x£Љ50 | 12 | b | |
…Ё≥ё–Ќ | ќе | x°Ё50 | 4 | c |
ЇѕЉ∆ | 1 | |||
£®1£©±н÷–a+b+c£љ°° °°£їm£љ°° °°£ї±Њіќµч≤йє≤Ћжїъ≥й»°ЅЋ°° °°√ыЌђ—І£ї
£®2£©‘Џ…»–ќЌ≥Љ∆ЌЉ÷–£ђ°∞Єї„г–Ќ°±ґ‘”¶µƒ…»–ќµƒ‘≤–ƒљ«µƒґ» э «°° °°£ї
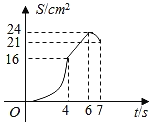
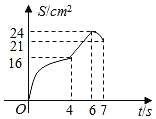
£®3£©єјЉ∆љсƒк5‘¬ЈЁ»Ђ–£Ѕгї®«Ѓ÷І≥ц‘Џ30°№x£Љ40ЈґќІƒЏµƒ—І…ъ»Ћ э£ї
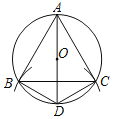
£®4£©‘Џ≥й—щµƒ°∞…Ё≥ё–Ќ°±—І…ъ÷–£ђ”–2√ы≈Ѓ…ъЇЌ2√ыƒ–…ъ£Ѓ—І–£Ќ≈ќѓЉ∆їЃі”÷–Ћжїъ≥й»°2√ыЌђ—І≤ќЉ”°∞¬ћ√зјн≤∆Љ∆їЃ°±їоґѓ£ђ«л‘Ћ”√ ч„іЌЉїт’яЅ–±нЋµ√ч«°Ї√≥йµљ“їƒ–“ї≈ЃµƒЄ≈¬ £Ѓ
°Њір∞Є°њ£®1£©0.5£ђ2£ђ40£ї£®2£©162°г£ї£®3£©120»Ћ£ї£®4£©![]()
°Њљвќц°њ
£®1£©”…x£Љ10µƒ»Ћ эЉ∞∆д∆µ¬ њ…µ√„№»Ћ э£ђ„№»Ћ э≥Ћ“‘20°№x£Љ40µƒ∞ўЈ÷±»£ђ‘ўЉх»•20°№x£Љ30µƒ»Ћ эЉіњ…µ√mµƒ÷µ£ђЌђјнЉ∆Ћг≥цnµƒ÷µ£ї
£®2£©ЄщЊЁћв“в«уµ√n£љ360°г°Ѕ°∞30°№x£Љ40°∞ЇЌ40°№x£Љ50ЈґќІµƒ—І…ъ»Ћ эґ‘”¶±»јэЉіњ…µ√µљљб¬џ£ї
£®3£©„№»Ћ э≥Ћ“‘°∞30°№x£Љ40ЈґќІµƒ—І…ъ»Ћ эґ‘”¶±»јэЉіњ…µ√µљљб¬џ£ї
£®4£©Ѕ–±нµ√≥цЋщ”–µ»њ…ƒ№љбєы э£ђ‘ўјы”√Є≈¬ єЂ љЉ∆Ћгњ…µ√£Ѓ
љв£Ї£®1£©±н÷–a+b+c£љ1©Б£®0.05+0.45£©£љ0.5£ї
±Њіќµч≤йµƒ„№»Ћ эќ™£®4+12+4£©°¬0.5£љ40£®»Ћ£©£ђ
m£љ40°Ѕ0.05£љ2£ђ
є ір∞Єќ™£Ї0.5£ђ2£ђ40£ї
£®2£©n£љ40°Ѕ0.45£љ6£ђ
°а°∞Єї„г–Ќ°±ґ‘”¶µƒ…»–ќµƒ‘≤–ƒљ«µƒґ» э «360°г°Ѕ![]() £љ162°г£ї
£љ162°г£ї
є ір∞Єќ™£Ї162°г£ї
£®3£©єјЉ∆Є√–£љсƒк5‘¬ЈЁЅг”√«Ѓ÷І≥ц‘Џ°∞30°№x£Љ40ЈґќІµƒ—І…ъ»Ћ э‘Љќ™800°Ѕ![]() £љ120£®»Ћ£©£ї
£љ120£®»Ћ£©£ї
£®4£©ї≠ ч„іЌЉќ™£Ї
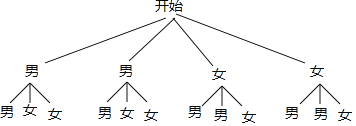
є≤”–12÷÷µ»њ…ƒ№µƒљбєы э£ђ∆д÷–≥й»°µƒЅљ»Ћ«°Ї√ «“ї√ыƒ–…ъЇЌ“ї√ы≈Ѓ…ъљбєы эќ™8£ђ
Ћщ“‘≥й»°µƒЅљ»Ћ«°Ї√ «“ї√ыƒ–…ъЇЌ“ї√ы≈Ѓ…ъЄ≈¬ £љ![]() £љ
£љ![]() £Ѓ
£Ѓ

 ‘ƒґЅњм≥µѕµЅ–ір∞Є
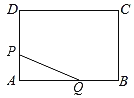
‘ƒґЅњм≥µѕµЅ–ір∞Є°Њћвƒњ°њ![]() »эќї≈ЃЌђ—ІЊЇ—°—І–£ЉіљЂ„й÷ѓµƒ°∞÷–єъ√ќ£ђќ“µƒ√ќ°±ќƒ“’—Ё≥ц≈Ѓ÷ч≥÷»Ћ£ђЋь√«µƒ± ‘≥…Љ®ЇЌњЏ ‘≥…Љ®°Ґ–ќѕуµ√Ј÷£ђЈ÷±р»зѕ¬£Ї
»эќї≈ЃЌђ—ІЊЇ—°—І–£ЉіљЂ„й÷ѓµƒ°∞÷–єъ√ќ£ђќ“µƒ√ќ°±ќƒ“’—Ё≥ц≈Ѓ÷ч≥÷»Ћ£ђЋь√«µƒ± ‘≥…Љ®ЇЌњЏ ‘≥…Љ®°Ґ–ќѕуµ√Ј÷£ђЈ÷±р»зѕ¬£Ї
|
|
| |
± ‘ |
|
|
|
њЏ ‘ |
|
|
|
–ќѕу |
|
|
|
∆љЊщЈ÷ |
|
|
|
£®1£©Ґў![]() £ї
£ї
ҐЏ‘Џ±нЄс÷–µƒ![]() Єц эµƒ÷–ќї э « £ђ÷Џ э «
Єц эµƒ÷–ќї э « £ђ÷Џ э «
£®2£©Њ≠—І–£—–ЊњЊцґ®£ђ‘Џ![]() ЅљќїЌђ—І÷–—°“їќї£Ѓ∆ј±»ЈљЈ®£Ї∞і± ‘≥…Љ®£ЇњЏ ‘≥…Љ®£Ї–ќѕуµ√Ј÷
ЅљќїЌђ—І÷–—°“їќї£Ѓ∆ј±»ЈљЈ®£Ї∞і± ‘≥…Љ®£ЇњЏ ‘≥…Љ®£Ї–ќѕуµ√Ј÷![]() љш––Љ∆Ћг£ђµ√Ј÷„оЄяµƒЌђ—Іќ™±Њіќќƒ“’—Ё≥цµƒ≈Ѓ÷ч≥÷»Ћ£Ѓ«лƒгЋг“їЋгƒƒќїЌђ—І„оЇу±ї—°ќ™±Њіќќƒ“’—Ё≥цµƒ≈Ѓ÷ч≥÷»Ћ£њ
љш––Љ∆Ћг£ђµ√Ј÷„оЄяµƒЌђ—Іќ™±Њіќќƒ“’—Ё≥цµƒ≈Ѓ÷ч≥÷»Ћ£Ѓ«лƒгЋг“їЋгƒƒќїЌђ—І„оЇу±ї—°ќ™±Њіќќƒ“’—Ё≥цµƒ≈Ѓ÷ч≥÷»Ћ£њ