题目内容
【题目】某商店通过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如表:
第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
调整前的单价x(元) | x1 | x2=6 | x3=72 | x4 | … | xn |
调整后的单价y(元) | y1 | y2=4 | y3=59 | y4 | … | yn |
已知这n个玩具调整后的单价都大于2元.
(1)求y与x的函数关系式,并确定x的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这n个玩具调整前、后的平均单价分别为 ![]() ,
, ![]() ,猜想
,猜想 ![]() 与
与 ![]() 的关系式,并写出推导过程.
的关系式,并写出推导过程.
【答案】
(1)解:设y=kx+b,由题意得x=6,y=4,x=72,y=59,
∴ ![]()
,解得 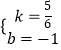 ,
,
∴y与x的函数关系式为y= ![]() x﹣1,
x﹣1,
∵这n个玩具调整后的单价都大于2元,
∴ ![]() x﹣1>2,解得x>
x﹣1>2,解得x> ![]() ,
,
∴x的取值范围是x> ![]()
(2)解:将x=108代入y= ![]() x﹣1得y=
x﹣1得y= ![]() ×108﹣1=89,
×108﹣1=89,
108﹣89=19,
答:顾客购买这个玩具省了19元
(3)解: ![]() =
= ![]()
![]() ﹣1,
﹣1,
推导过程:由(1)得y1= ![]() x1﹣1,y2=
x1﹣1,y2= ![]() x2﹣1,…yn=
x2﹣1,…yn= ![]() xn﹣1,
xn﹣1,
∴ ![]() =
= ![]() (y1+y2+…+yn)=
(y1+y2+…+yn)= ![]() [(
[( ![]() x1﹣1)+(
x1﹣1)+( ![]() x2﹣1)+…+(
x2﹣1)+…+( ![]() xn﹣1)]=
xn﹣1)]= ![]() [
[ ![]() (x1+x2+…+xn)﹣n]=
(x1+x2+…+xn)﹣n]= ![]() ×
× ![]() ﹣1=
﹣1= ![]()
![]() ﹣1
﹣1
【解析】(1)设y=kx+b,根据题意列方程组即可得到结论,再根据已知条件得到不等式于是得到x的取值范围是x> ![]() ;(2)将x=108代入y=
;(2)将x=108代入y= ![]() x﹣1即可得到结论;(3)由(1)得y1=
x﹣1即可得到结论;(3)由(1)得y1= ![]() x1﹣1,y2=
x1﹣1,y2= ![]() x2﹣2,…yn=
x2﹣2,…yn= ![]() xn﹣1,根据求平均数的公式即可得到结论.
xn﹣1,根据求平均数的公式即可得到结论.

【题目】在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,当5≤m<10时为B级,当0≤m<5时为C级.现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下表:
11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 |
2 | 8 | 10 | 17 | 6 | 13 | 7 | 5 | 7 | 3 |
12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(1)求样本数据中为A级的频率;
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取2人,用列举法求抽得2个人的“日均发微博条数”都是3的概率.