题目内容
【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，其对称轴为x=1，则下列结论中错误的是（ ）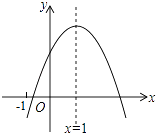 
A.abc＜0
B.a﹣b+c＜0
C.b2﹣4ac＞0
D.3a+c＞0
【答案】D
【解析】解：A、由抛物线开口向下，可得a＜0， 由抛物线与y轴的交点在x轴的上方，可得c＞0，
由抛物线的对称轴为x=1，可得﹣ 
＞0，则b＞0，
∴abc＜0，故A正确，不符合题意；
B．当x=﹣1时，y＜0，则a﹣b+c＜0，故B正确，不符合题意；
C．由抛物线与x轴有两个交点，可得b2﹣4ac＞0，故C正确，不符合题意；
D．∵对称轴x=﹣ =1，
∴b=﹣2a，
∵a﹣b+c＜0，
∴3a+c＜0，
故D错误，符合题意；
故选D．
【考点精析】根据题目的已知条件，利用二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案，需要掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．
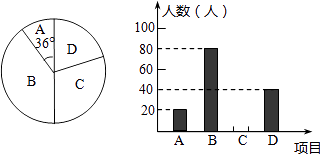
【题目】九（2）班体育委员用划记法统计本班40名同学投掷实心球的成绩，结果如图所示：则这40名同学投掷实心球的成绩的众数和中位数分别是（ ）
成绩 | 6 | 7 | 8 | 9 | 10 |
人数 |
| 正 | 正 | 正 | 正 |
A.8，8
B.8，8.5
C.9，8
D.9，8.5
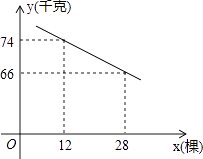
【题目】某商店通过调低价格的方式促销n个不同的玩具，调整后的单价y（元）与调整前的单价x（元）满足一次函数关系，如表：
第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
调整前的单价x（元） | x1 | x2=6 | x3=72 | x4 | … | xn |
调整后的单价y（元） | y1 | y2=4 | y3=59 | y4 | … | yn |
已知这n个玩具调整后的单价都大于2元．
（1）求y与x的函数关系式，并确定x的取值范围；
（2）某个玩具调整前单价是108元，顾客购买这个玩具省了多少钱？
（3）这n个玩具调整前、后的平均单价分别为 
， 
，猜想 与 的关系式，并写出推导过程．
