Question

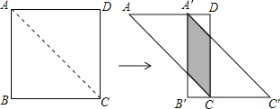
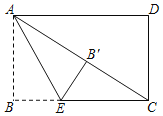
【题目】如图，在矩形ABCD中，AB＝1，BC＝2，点E在边BC上，将△ABE沿AE折叠，点B恰好落在对角线AC上的点B′处．则线段BE的长为_____．

Answer 1

【答案】．

【解析】

由矩形的性质和勾股定理可求得AC的长；根据折叠的性质知BE＝B′E，AB＝AB′＝1，∠AB'E＝∠B＝90°；设BE＝x，可用x分别表示出B′E和EC，在Rt△B′EC中，根据勾股定理求得BE的长．

解：∵四边形ABCD是矩形，

∴∠B＝90°，

∴AC＝＝＝，

由折叠的性质得：BE'＝BE，AB'＝AB＝1，∠AB'E＝∠B＝90°，

∴B'C＝AC﹣AB'＝﹣1，∠CB'E＝90°，

设BE＝x，则B'E＝x，CE＝2﹣x，

在Rt△CEB'中，B'E2+B'C2＝CE2，

即x2+（﹣1）2＝（2﹣x）2，

解得：x＝，

∴BE＝，

故答案为：．