题目内容
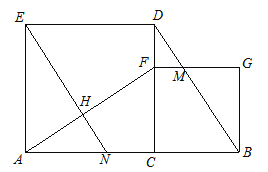
【题目】如图,在平面直角坐标系中,抛物线![]() (a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(1)求抛物线的解析式;
(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点N从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN的面积为S,点M运动时间为t,试求S与t的函数关系,并求S的最大值;
(3)在点M运动过程中,是否存在某一时刻t,使△MBN为直角三角形?若存在,求出t值;若不存在,请说明理由.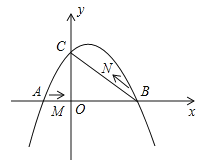
【答案】(1)![]() ;(2)S=
;(2)S=![]() ,运动1秒使△PBQ的面积最大,最大面积是
,运动1秒使△PBQ的面积最大,最大面积是![]() ;(3)t=
;(3)t=![]() 或t=
或t=![]() .
.
【解析】
(1)把点A、B、C的坐标分别代入抛物线解析式,列出关于系数a、b、c的解析式,通过解方程组求得它们的值;
(2)设运动时间为t秒.利用三角形的面积公式列出S△MBN与t的函数关系式.利用二次函数的图象性质进行解答;
(3)根据余弦函数,可得关于t的方程,解方程,可得答案.
(1)∵点B坐标为(4,0),抛物线的对称轴方程为x=1,
∴A(﹣2,0),把点A(﹣2,0)、B(4,0)、点C(0,3),
分别代入![]() (a≠0),得:
(a≠0),得:![]() ,解得:
,解得: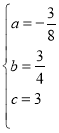 ,所以该抛物线的解析式为:
,所以该抛物线的解析式为:![]() ;
;
(2)设运动时间为t秒,则AM=3t,BN=t,∴MB=6﹣3t.
由题意得,点C的坐标为(0,3).在Rt△BOC中,BC=![]() =5.
=5.
如图1,过点N作NH⊥AB于点H,
∴NH∥CO,
∴△BHN∽△BOC,
∴![]() ,即
,即![]() ,
,
∴HN=![]() t,
t,
∴S△MBN=![]() MBHN=
MBHN=![]() (6﹣3t)
(6﹣3t)![]() t,
t,
即S=![]()
![]() ,
,
当△PBQ存在时,0<t<2,
∴当t=1时,S△PBQ最大=![]() .
.
答:运动1秒使△PBQ的面积最大,最大面积是![]() ;
;
(3)如图2,在Rt△OBC中,cos∠B=![]() .
.
设运动时间为t秒,则AM=3t,BN=t,∴MB=6﹣3t.
①当∠MNB=90°时,cos∠B=![]() ,即
,即![]() ,化简,得17t=24,解得t=
,化简,得17t=24,解得t=![]() ;
;
②当∠BMN=90°时,cos∠B=![]() ,化简,得19t=30,解得t=
,化简,得19t=30,解得t=![]() .
.
综上所述:t=![]() 或t=
或t=![]() 时,△MBN为直角三角形.
时,△MBN为直角三角形.

【题目】广宇、承义两名同学分别进行5次射击训练,训练成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
广宇 | 9 | 8 | 7 | 7 | 9 |
承义 | 6 | 8 | 10 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A.广宇训练成绩的平均数大于承义训练成绩平均数
B.广宇训练成绩的中位数与承义训练成绩中位数不同
C.广宇训练成绩的众数与承义训练成绩众数相同
D.广宇训练成绩比承义训练成绩更加稳定
【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
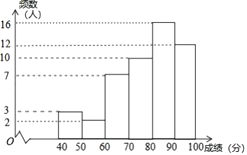
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.