题目内容
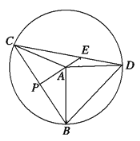
【题目】已知![]() 是一张直角三角形纸片,其中
是一张直角三角形纸片,其中![]() ,
,![]() ,小亮将它绕点
,小亮将它绕点![]() 逆时针旋转后
逆时针旋转后![]() 得到
得到![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.

(1)如图1,当![]() 时,
时,![]() 所在直线与线段
所在直线与线段![]() 有怎样的位置关系?请说明理由.
有怎样的位置关系?请说明理由.
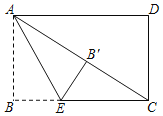
(2)如图2,当![]() ,求
,求![]() 为等腰三角形时的度数.
为等腰三角形时的度数.
【答案】(1)BD与FM互相垂直,理由见解析;(2)β的度数为30°或75°或120°.
【解析】
(1)由题意设直线BD与FM相交于点N,即可根据旋转的性质判断直线BD与线段MF垂直;
(2)根据旋转的性质得∠MAD=β,分类讨论:当KA=KD时,根据等腰三角形的性质得∠KAD=∠D=30°,即β=30°;当DK=DA时,根据等腰三角形的性质得∠DKA=∠DAK,然后根据三角形内角和可计算出∠DAK=75°,即β=75°;当AK=AD时,根据等腰三角形的性质得∠AKD=∠D=30°,然后根据三角形内角和可计算出∠KAD=120°,即β=120°.
解:(1)BD与FM互相垂直,理由如下
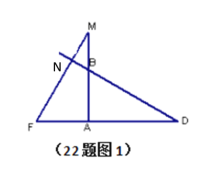
设此时直线BD与FM相交于点N
∵∠DAB=90°,∠D=30°
∴∠ABD=90°-∠D=60°,
∴∠NBM=∠ABD=60°
由旋转的性质得△ADB≌△AMF,∴∠D=∠M=30°
∴∠MNB=180°-∠M-∠NBM=180°-30°- 60°= 90°
∴BD与FM互相垂直
(2)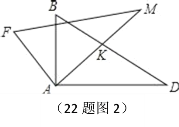
当KA=KD时,则∠KAD=∠D=30°,即β=30°;
当DK=DA时,则∠DKA=∠DAK,
∵∠D=30°,∴∠DAK=(180°﹣30°)÷2=75°,即β=75°;
当AK=AD时,则∠AKD=∠D=30°,
∴∠KAD=180°﹣30°﹣30°=120°,即β=120°,
综上所述,β的度数为30°或75°或120°.

练习册系列答案
相关题目