题目内容
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴的交点为A,B(点A 在点B的左侧).
轴的交点为A,B(点A 在点B的左侧).
(1)求点A,B的坐标;
(2)横、纵坐标都是整数的点叫整点.
①直接写出线段AB上整点的个数;
②将抛物线![]() 沿
沿![]() 翻折,得到新抛物线,直接写出新抛物线在
翻折,得到新抛物线,直接写出新抛物线在![]() 轴上方的部分与线段
轴上方的部分与线段![]() 所围成的区域内(包括边界)整点的个数.
所围成的区域内(包括边界)整点的个数.
【答案】(1)点A的坐标为(-1,0),点B的坐标为(3,0)(2)①5;②6.
【解析】
(1)根据x轴上的点的坐标特征即y=0,可得关于x的方程,解方程即可;
(2)①直接写出从-1到3的整数的个数即可;
②先确定新抛物线的解析式,进而可得其顶点坐标,再结合函数图象解答即可.
解:(1)在![]() 中 ,令y=0,
中 ,令y=0,![]() ,解得:
,解得:![]() ,
,
∴点A的坐标为(-1,0),点B的坐标为(3,0);
(2)①线段AB之间横、纵坐标都是整数的点有(-1,0)、(0,0)、(1,0)、(2,0)、(3,0).
∴线段AB上一共有5个整点;
②抛物线![]() 沿
沿![]() 翻折,得到的新抛物线是
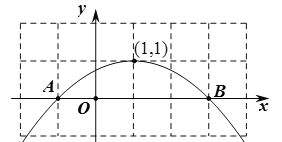
翻折,得到的新抛物线是![]() ,如图,其顶点坐标是(1,1),
,如图,其顶点坐标是(1,1),
观察图象可知:线段AB上有5个整点,顶点为1个整点,新抛物线在![]() 轴上方的部分与线段
轴上方的部分与线段![]() 所围成的区域内(包括边界)共6个整点.
所围成的区域内(包括边界)共6个整点.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目