题目内容
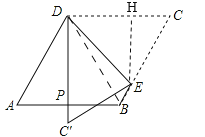
【题目】如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB的中点)所在的直线上,得到经过点D的折痕DE,若菱形边长为1,则点E到CD的距离为_____.

【答案】![]()
【解析】
连接BD,过E作EH垂直于CD于点H.由菱形的性质及∠A=60°,得到三角形ABD为等边三角形,P为AB的中点,利用三线合一得到DP为角平分线,得到∠ADP=30°,∠ADC=120°,∠C=60°,进而求出∠PDC=90°,由折叠的性质得到∠CDE=∠PDE=45°.再设EH=x,表示出DH,CH,列出方程求解即可得.
解:连接BD,过E作EH垂直于CD于点H.
四边形ABCD为菱形,∠A=60°,
∴△ABD为等边三角形,∠ADC=120°,∠C=60°,
∵P为AB的中点,
∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°,
∴∠PDC=90°,
∴由折叠的性质得到∠CDE=∠PDE=45°,设EH=x,
则DH=EH=x,
∠C=60°,则∠CEH=30°,EC=2CH,
由勾股定理可得:![]() ,
,
∵DH+CH=CD=1,
∴![]() ,解得
,解得![]()
即点E到CD的距离为![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目