题目内容
【题目】已知二次函数y=﹣x2+4x.
(1)写出二次函数y=﹣x2+4x图象的对称轴;
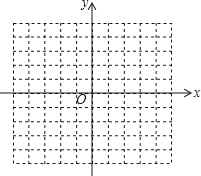
(2)在给定的平面直角坐标系中,画出这个函数的图象(列表、描点、连线);
(3)根据图象,写出当y<0时,x的取值范围.
【答案】(1)对称轴是过点(2,4)且平行于y轴的直线x=2;(2)见解析;(3)x<0或x>4.
【解析】试题分析:(1)把一般式化成顶点式即可求得;
(2)首先列表求出图象上点的坐标,进而描点连线画出图象即可.
(3)根据图象从而得出y<0时,x的取值范围.
试题解析:(1)∵y=-x2+4x=-(x-2)2+4,
∴对称轴是过点(2,4)且平行于y轴的直线x=2;
(2)列表得:
x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | -5 | 0 | 3 | 4 | 3 | 0 | -5 | … |
描点,连线.
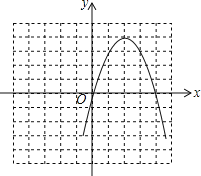
(3)由图象可知,
当y<0时,x的取值范围是x<0或x>4.

练习册系列答案
相关题目