题目内容
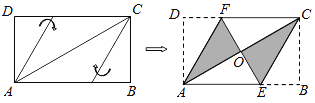
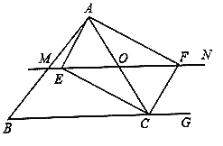
【题目】如图,在![]() 中,点
中,点![]() 为边
为边![]() 上的一个动点,过点
上的一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的外角平分线
的外角平分线![]() 于点
于点![]() ,交
,交![]() 的角平分线
的角平分线![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论;
是矩形?并证明你的结论;
【答案】(1)见解析; (2)当点![]() 运动到
运动到![]() 中点即
中点即![]() 时,四边形
时,四边形![]() 是矩形. 证明见解析.
是矩形. 证明见解析.
【解析】
(1)根据平行线性质和角平分线性质求出∠OCE=∠OEC,推出OC=OE,同理求出OC=OF即可;
(2)根据平行四边形的判定以及矩形的判定得出即可;
解:(1):∵MN∥BC,
∴∠OEC=∠ECB,
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴∠OCE=∠OEC,
∴OC=OE,
同理OC=OF,
∴OE=OF;
(2)当点![]() 运动到
运动到![]() 中点即
中点即![]() 时,四边形
时,四边形![]() 是矩形,理由如下:
是矩形,理由如下:
由(1)知,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 是
是![]() 的角平分线,
的角平分线,![]() 是
是![]() 的角平分线,
的角平分线,
![]() ,
,
即![]() ,
,
![]() 四边形
四边形![]() 是矩形.
是矩形.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目