题目内容
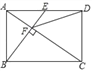
【题目】如图,E是矩形ABCD的边AD的中点,且BE⊥AC交于点F,则下列结论中正确的是( )
A. CF=3AF
B. △DCF是等边三角形
C. 图中与△AEF相似的三角形共有4个
D. tan∠CAD=![]()
【答案】D
【解析】分析:由![]() 又AD∥BC,所以
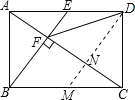
又AD∥BC,所以![]() 故A错误,不符合题意;过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出
故A错误,不符合题意;过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出![]() 得到CN=NF,根据线段的垂直平分线的性质可得结论,故B错误,不符合题意;根据相似三角形的判定即可求解,故C错误,不符合题意;由△BAE∽△ADC,得到CD与AD的大小关系,根据正切函数可求tan∠CAD的值,故D正确,符合题意.
得到CN=NF,根据线段的垂直平分线的性质可得结论,故B错误,不符合题意;根据相似三角形的判定即可求解,故C错误,不符合题意;由△BAE∽△ADC,得到CD与AD的大小关系,根据正切函数可求tan∠CAD的值,故D正确,符合题意.
详解:A.∵AD∥BC,
∴△AEF∽△CBF,
∴![]() ∵
∵![]()
∴![]() 故A错误,不符合题意;
故A错误,不符合题意;
B. 过D作DM∥BE交AC于N,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴![]()
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DF=DC,
∴![]() 是等腰三角形,无法判定是等边三角形,
是等腰三角形,无法判定是等边三角形,
故B错误,不符合题意;
C. 图中与△AEF相似的三角形有△ACD,△BAF,△CBF,△CAB,△BEA共有5个,故C错误,不符合题意;
D. 设AD=a,AB=b由△BAE∽△ADC,有![]()
∵![]()
故D正确,符合题意.
故选D.

【题目】利民商场经营某种品牌的T恤,购进时的单价是300元,根据市场调查:在一段时间内,销售单价是400元时,销售量是60件,销售单价每涨10元,销售量就减少1件.设这种T恤的销售单价为x元(x>400)时,销售量为y件、销售利润为W元.
(1)请分别用含x的代数式表示y和W(把结果填入下表):
销售单价(元) | x |
销售量y(件) | |
销售利润W(元) |
(2)该商场计划实现销售利润10000元,并尽可能增加销售量,那么x的值应当是多少?