Question

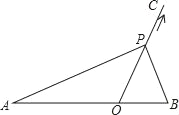
【题目】如图，点O在线段AB上，AO＝2，OB＝1，OC为射线，且∠BOC＝60°，动点P以每秒2个单位长度的速度从点O出发，沿射线OC做匀速运动，设运动时间为t秒．当△ABP是直角三角形时，t的值为（　　）

A. B. C. 1或 D. 1或

Answer 1

【答案】C

【解析】

根据题意分三种情况考虑：当∠A=90°；当∠B=90°；当∠APB=90°，根据△ABP为直角三角形，分别求出t的值即可．

解：分三种情况考虑：

当∠A＝90°，即△ABP为直角三角形时，

∵∠BOC＞∠A，且∠BOC＝60°，

∴∠A≠90°，故此情况不存在；

当∠B＝90°，即△ABP为直角三角形时，如图所示：

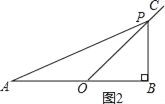
∵∠BOC＝60°，

∴∠BPO＝30°，

∴OP＝2OB＝2，

∵OP＝2t，

∴t＝1；

当∠APB＝90°，即△ABP为直角三角形时，过P作PD⊥AB，

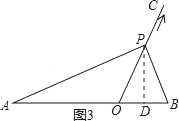
∴OD＝OPcos∠BOC＝t，PD＝OPsin∠BOC＝t，

∴AD＝AO+OD＝2+t，BD＝OB﹣OD＝1﹣t，即AB＝3，

在Rt△ABP中，根据勾股定理得：

AP2+BP2＝AB2，即（2+t）2+（t）2+（t）2+（1﹣t）2＝32，

解得：t＝或（负值舍去），

综上，当t ＝1或t＝时，△ABP是直角三角形．

故选：C．