题目内容
(本题满分8分)如图,在正方形ABCD中,E是AB边上任意一点,BG⊥CE,垂足为点O,交AC于点F,交AD于点G。
(1)证明:BE="AG" ;
(2)点E位于什么位置时,∠AEF=∠CEB,说明理由。
(1)证明:BE="AG" ;
(2)点E位于什么位置时,∠AEF=∠CEB,说明理由。

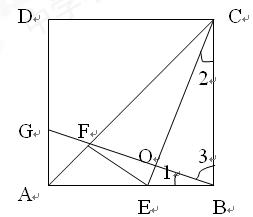
(1)证明:∵四边形ABCD是正方形
∴∠ABC=∠BAD=90°,∴∠1+∠3=90°,
∵BG⊥CE,∴∠BOC=90°∴∠2+∠3=90°,
∴∠1=∠2 ………………………2分
在△GAB和△EBC中,
∵∠GAB=∠EBC=90°,AB=BC,∠1=∠2
∴△GAB≌△EBC (ASA)
∴AG="BE " ………………………… 4分
(2)解:当点E位于线段AB中点时,∠AEF=∠CEB …… 5分
理由如下:若当点E位于线段AB中点时,则AE=BE,
由(1)可知,AG=BE
 ∴AG="AE " …………………… 6分
∴AG="AE " …………………… 6分∵四边形ABCD是正方形,∴∠GAF=∠EAF=45°
又∵AF=AF,∴△GAF≌△EAF (SAS)
∴∠AGF=∠AEF ………………………………………7分
由(1)知,△GAB≌△EBC
 ∴∠AGF=∠CEB,
∴∠AGF=∠CEB,∴∠AEF=∠CEB ………………………………… 8分
略

练习册系列答案
相关题目
 AD,且BE=CF.
AD,且BE=CF.

 中,
中,
 则
则 的值是
的值是

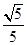




 填空:
填空:


