题目内容
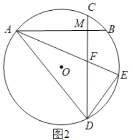
【题目】如图，在△ABC中，∠BOC＝140°，I是内心，O是外心，则∠BIC等于（ ）
A.130°B.125°C.120°D.115°
【答案】B
【解析】
根据圆周角定理求出∠BOC=2∠A，求出∠A度数，根据三角形内角和定理求出∠ABC+∠ACB，根据三角形的内心得出∠IBC=
∠ABC，∠ICB=∠ACB，求出∠IBC+∠ICB的度数，再求出答案即可.
∵在△ABC中，∠BOC=140°，O是外心，
∴∠BOC=2∠A，
∴∠A=70°，
∴∠ABC+∠ACB=180°﹣∠A=110°，
∵I为△ABC的内心，
∴∠IBC=∠ABC，∠ICB=∠ACB，
∴∠IBC+∠ICB=
=55°，
∴∠BIC=180°﹣（∠IBC+∠ICB）=125°，
故选：B.
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
【题目】某校为了解学生课外阅读情况，就学生每周阅读时间随机调查了部分学生，调查结果按性别整理如下：
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
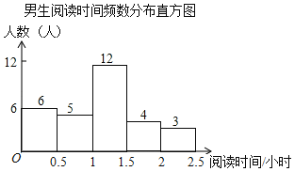
根据图表解答下列问题：
（1）在女生阅读时间人数统计表中，
，
；
（2）此次抽样调查中，共抽取了 名学生，学生阅读时间的中位数在 时间段；
（3）从阅读时间在2～2.5小时的5名学生中随机抽取2名学生参加市级阅读活动，恰好抽到男女生各一名的概率是多少？
