题目内容
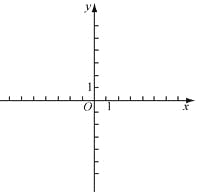
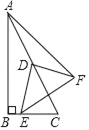
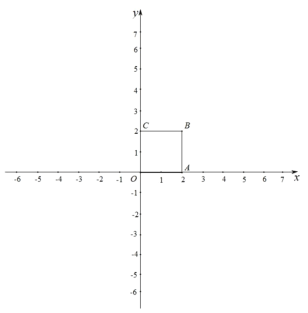
【题目】对于平面内的点 P 和图形 M，给出如下定义：以点 P 为圆心，以 r 为半径作⊙P，使得图形 M 上的所有点都在⊙P 的内部（或边上），当 r 最小时，称⊙P 为图形 M 的 P 点 控制圆，此时，⊙P 的半径称为图形 M 的 P 点控制半径．已知，在平面直角坐标系中， 正方形 OABC 的位置如图所示，其中点 B（2，2）
（1）已知点 D（1，0），正方形 OABC 的 D 点控制半径为 r1，正方形 OABC 的 A 点 控制半径为 r2，请比较大小：r1 r2；
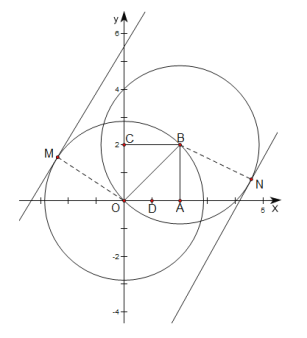
（2）连接 OB，点 F 是线段 OB 上的点，直线 l：y= 
x+b；若存在正方形 OABC 的 F点控制圆与直线 l 有两个交点，求 b 的取值范围．
【答案】（1）＜；（2）
．
【解析】
（1）根据控制半径的定义求出r1和r2即可解决问题；
（2）如图所示，圆O和圆B分别是以O，B为圆心，以OB长为半径的圆，分别求出直线l与圆O相切，直线l与圆B相切时的b值，得到两种极限情况下的b值，即可得到b 的取值范围．
解：（1）由题意得：r1＝BD＝CD＝
，r2＝AC＝
，
∴r1＜r2；
（2）如图所示，圆O和圆B分别是以O，B为圆心，以OB长为半径的圆，
当直线l：
与圆O相切于点M时，连接OM，可得OM与直线l垂直，
则直线OM的解析式为：
，
设M（x，
），
∵OM＝OB，
∴OM＝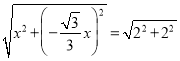
，
∴
或
（舍去），
∴M（
，
），
将（，）代入得：
，
解得：
，
当直线l：与圆B相切于点N时，连接BN，
同理可求出此时
，
∴b的取值范围为：．
【题目】某市对即将参加中考的4000名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和不完整的频数分布直方图．请根据图表信息回答下列问题：
初中毕业生视力抽样调查频数分布表
视力 | 频数（人） | 频率 |
4.0≤x＜4.3 | 20 | 0.1 |
4.3≤x＜4.6 | 40 | 0.2 |
4.6≤x＜4.9 | 70 | 0.35 |
4.9≤x＜5.2 | a | 0.3 |
5.2≤x＜5.5 | 10 | b |
（1）本次调查样本容量为 ；
（2）在频数分布表中，a＝ ，b＝ ，并将频数分布直方图补充完整；
（3）若视力在4.9以上（含4.9）均属标准视力，根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人？
