题目内容
【题目】已知：⊙O的两条弦AB，CD相交于点M，且AB=CD．
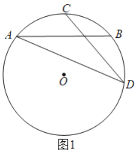
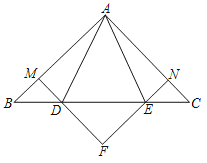
（1）如图1，连接AD．求证：AM=DM．
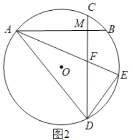
（2）如图2，若AB⊥CD，在弧BD上取一点E，使弧BE=弧BC，AE交CD于点F，连AD、DE．
①利断∠E与∠DFE是否相等，并说明理由．
②若DE=7，AM+MF=17，求△ADF的面积．
【答案】（1）详见解析；（2）①
，理由详见解析；②42
【解析】
（1）由弦相等得到弧相等，从而可得到
，因此
，从而得证；
（2）①连接
，由弧相等可得到
，再由
可得到
，在通过同弧所对的圆周角相等可知
，等量代换即可；②由得到
，再通过
，即可推出
，然后即可算出△ADF的面积．
（1）∵
∴
∴
即
∴
∴
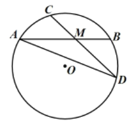
（2）①
连接，
∵
∴
∵
∴
∴
∵，
∴
②∵
∴
∵
∴
∵
∴
∴
的面积
练习册系列答案
相关题目
【题目】表中所列
、
的7对值是二次函数
图象上的点所对应的坐标，其中
| … |
|
|
|
|
|
|
| … |
| … | 6 |
| 11 |
| 11 |
| 6 | … |
根据表中提供约信息，有以下4个判断：①
；②
；③当
时，的值是
；④
；其中判断正确的是（ ）
A.①②③B.①②④C.①③④D.②③④
