题目内容
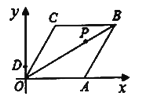
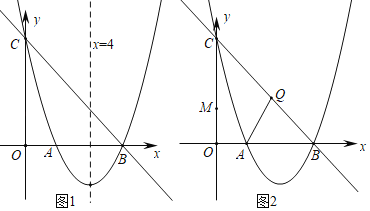
【题目】如图1所示,已知直线y=kx+m与抛物线y=ax2+bx+c分别交于x轴和y轴上同一点,交点分别是点B(6,0)和点C(0,6),且抛物线的对称轴为直线x=4;
(1)试确定抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PBC是直角三角形?若存在请直接写出P点坐标,不存在请说明理由;
(3)如图2,点Q是线段BC上一点,且CQ=![]() ,点M是y轴上一个动点,求△AQM的最小周长.
,点M是y轴上一个动点,求△AQM的最小周长.
【答案】(1)y=![]() ;(2)存在,点P的坐标为(4,﹣2)或(4,10)或(4,3+
;(2)存在,点P的坐标为(4,﹣2)或(4,10)或(4,3+![]() )或P(4,3﹣
)或P(4,3﹣![]() );(3)4
);(3)4![]() .
.
【解析】
(1)求得点A的坐标,根据抛物线过点A、B、C三点,从而可以求得抛物线的解析式;
(2))△ABP为直角三角形时,分别以三个顶点为直角顶点讨论:根据直角三角形的性质和勾股定理列方程解决问题;
(3)求出点Q的坐标为(![]() ),在x轴上取点G(﹣2,0),连接QG交y轴于点M,则此时△AQM的周长最小,求出QG+AQ的值即可得出答案.
),在x轴上取点G(﹣2,0),连接QG交y轴于点M,则此时△AQM的周长最小,求出QG+AQ的值即可得出答案.
解:(1)∵抛物线y=ax2+bx+c与x轴交于点A、B两点,对称轴为直线x=4,
∴点A的坐标为(2,0).
∵抛物线y=ax2+bx+c过点A(2,0),B(6,0),C(0,6),
解得a=![]() ,b=﹣4,c=6.
,b=﹣4,c=6.
∴抛物线的解析式为:y=![]() ;
;
(2)设P(4,y),
∵B(6,0),C(0,6),
∴BC2=62+62=72,PB2=22+y2,PC2=42+(y﹣6)2,
当∠PBC=90°时,BC2+PB2=PC2,
∴72+22+y2=42+(y﹣6)2,
解得:y=﹣2,
∴P(4,﹣2);
当∠PCB=90°时,PC2+BC2=PB2,
∴42+(y﹣6)2+72=22+y2,
解得:y=10,
∴P(4,10);
当∠BPC=90°时,PC2+PB2=BC2.
∴42+(y﹣6)2+22+y2=72,
解得:y=![]() .
.
∴P(4,![]() )或P(4,
)或P(4,![]() ).
).
综合以上可得点P的坐标为(4,﹣2)或(4,10)或(4,3+![]() )或P(4,3﹣
)或P(4,3﹣![]() ).
).
(3)过点Q作QH⊥y轴于点H,
∵B(6,0),C(0,6),
∴OB=6,OC=6,
∴∠OCB=45°,
∴∠CQH=∠HCQ=45°,
∵CQ=![]() ,
,
∴CH=QH=![]()
∴OH=![]()
∴点Q的坐标为(![]() ),
),
在x轴上取点G(﹣2,0),连接QG交y轴于点M,则此时△AQM的周长最小,
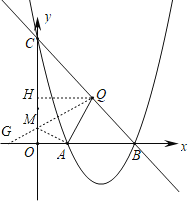
∴AQ=![]()
QG=![]()
∴AQ+QG=![]()
∴△AQM的最小周长为4![]() .
.

 名校课堂系列答案
名校课堂系列答案