题目内容
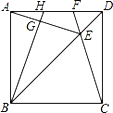
【题目】图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
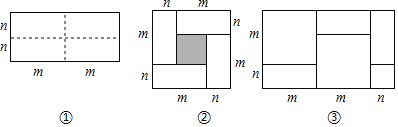
(1)图②中的阴影部分的面积为 .
(2)观察图②,三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系是 .
(3)若x+y=﹣6,xy=![]() ,则x﹣y= .
,则x﹣y= .
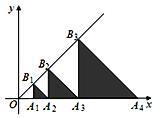
(4)观察图③,你能得到怎样的代数恒等式呢?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)图②中阴影部分为边长为![]() 的正方形,从而其面积可求;
的正方形,从而其面积可求;
(2)大正方形的面积减去长方形的面积可得阴影部分的面积,也可得出三个代数式![]() ,
,![]() ,
,![]() 之间的等量关系;
之间的等量关系;
(3)由(2)所得出的关系式,可求出![]() ,从而可求出
,从而可求出![]() 的值;
的值;
(4)利用两种不同的方法表示出大矩形的面积,即可得出等式.
解:(1)图②中阴影部分为边长为![]() 的正方形,其面积为:
的正方形,其面积为:![]()
故答案为:![]() .
.
(2)最外层大正方形的面积为:![]() ,4个长方形的面积为
,4个长方形的面积为![]() ,
,
阴影部分面积为![]() ,总体看图形的面积和分部分之和的面积相等
,总体看图形的面积和分部分之和的面积相等
故答案为:![]() .
.
(3)![]() ,
,![]() ,
,
![]()
![]()
故答案为:![]() .
.
(4)由整体求面积和分部分求面积,二者相等,可得:
![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目