题目内容
【题目】如图,△A1B1A2,△A2B2A3,△A3B3A4,...,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An,在x轴上,点B1、B2、…Bn在直线y=x上,已知OA1=1,则OA2019的长是_____.
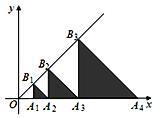
【答案】22018
【解析】
根据一次函数的性质可得∠B1OA1=45°,然后求出△OA2B2是等腰直角三角形,△OA3B2是等腰直角三角形,然后根据等腰直角三角形斜边上的高等于斜边的一半求出OA3,同理求出OA4,然后根据变化规律写出即可.
解:∵直线为y=x,
∴∠B1OA1=45°,
∵△A2B2A3,
∴B2A2⊥x轴,∠B2A3A2=45°,
∴△OA2B2是等腰直角三角形,△OA3B2是等腰直角三角形,
∴OA3=2A2B2=2OA2=2×2=4,
同理可求OA4=2OA3=2×4=23,
…,
所以,OA2019=22018.
故答案为:22018.

练习册系列答案
相关题目
【题目】随着科学技术的发展,信息化、网络化时代的到来,很多农产品改变了原来的销售模式,实行了网上销售,刚大学毕业的小韦把自己家的红薯产品也放到网上,他原来计划每天卖出150千克,由于各种原因,实际每天的销售量与计划量相比有出入,下表是国庆小长假期间的销售情况(超出部分记为正,不足记为负,单位:千克)
时间 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据上表前四天一共卖出了多少千克?
(2)销售量最多的一天与最少的一天分别是多少千克?
(3)若每千克按2. 6元出售,并需付运费平均每千克0. 3元,则小韦国庆小长假期间一共收入多少钱?