题目内容
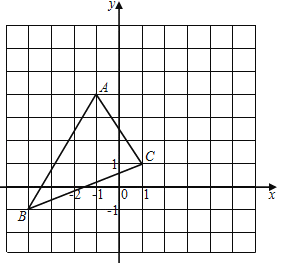
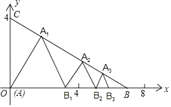
【题目】如图，已知，点A（0，0）、B（4
，0）、C（0，4），在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…则第2017个等边三角形的边长等于（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】根据锐角三函数的性质，由OB=
，OC=1，可得∠OCB=90°，然后根据等边三角形的性质，可知∠A1AB=60°，进而可得∠CAA1=30°，∠CA1O=90°，因此可推导出∠A2A1B=30°，同理得到∠CA2B1=∠CA3B2=∠CA4B3=90°，∠A2A1B=∠A3A2B2=∠A4A3B3=30°，故可得后一个等边三角形的边长等于前一个等边三角形的边长的一半，即OA1=OCcos∠CAA1=
，B1A2=
，以此类推，可知第2017个等边三角形的边长为：
.
故选：C.
【题目】某服装店用4400元购进A，B两种新式服装，按标价售出后可获得毛利润2800元（毛利润＝售价﹣进价），这两种服装的进价，标价如表所示．
类型价格 | A型 | B型 |
进价（元/件） | 60 | 100 |
标价（元/件） | 100 | 160 |
(1)请利用二元一次方程组求这两种服装各购进的件数；
(2)如果A种服装按标价的9折出售，B种服装按标价的8折出售，那么这批服装全部售完后，服装店比按标价出售少收入多少元？
【题目】已知某山区的平均气温与该山的海拔高度的关系见下表：
海拔高度（单位：米） | 0 | 100 | 200 | 300 | 400 | … |
平均气温（单位：℃） | 22 | 21.5 | 21 | 20.5 | 20 | … |
（1）若海拔高度用x（米）表示，平均气温用y（℃）表示，试写出y与x之间的函数关系式；
（2）若某种植物适宜生长在18℃～20℃（包含18℃，也包含20℃）山区，请问该植物适宜种植在海拔为多少米的山区？