题目内容
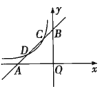
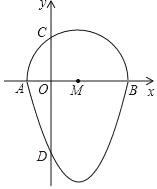
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2﹣6x﹣16,AB为半圆的直径,则这个“果圆”被y轴截得的线段CD的长为_____.
【答案】20
【解析】
抛物线的解析式为y=x2-6x-16,可以求出AB=10;在Rt△COM中可以求出CO=4;则:CD=CO+OD=4+16=20.
抛物线的解析式为y=x2-6x-16,
则D(0,-16)
令y=0,解得:x=-2或8,
函数的对称轴x=-![]() =3,即M(3,0),
=3,即M(3,0),
则A(-2,0)、B(8,0),则AB=10,
圆的半径为![]() AB=5,
AB=5,
在Rt△COM中,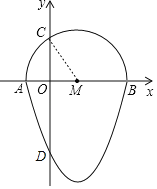
OM=5,OM=3,则:CO=4,
则:CD=CO+OD=4+16=20.
故答案是:20.

练习册系列答案
相关题目
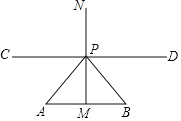
【题目】装潢公司要给边长为6米的正方形墙面ABCD进行装潢,设计图案如图所示(四周是四个全等的矩形,用材料甲进行装潢;中心区是正方形MNPQ,用材料乙进行装潢).
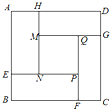
两种装潢材料的成本如下表:
材料 | 甲 | 乙 |
价格(元/米2) | 50 | 40 |
设矩形的较短边AH的长为x米,装潢材料的总费用为y元.
(1)MQ的长为 米(用含x的代数式表示);
(2)求y关于x的函数解析式;
(3)当中心区的边长不小于2米时,预备资金1760元购买材料一定够用吗?请说明理由.