题目内容
【题目】在平面直角坐标系中，点O（0，0），点A（1，0）．已知抛物线y＝x2+mx﹣2m（m是常数），顶点为P．
（Ⅰ）当抛物线经过点A时，求顶点P的坐标；
（Ⅱ）若点P在x轴下方，当∠AOP＝45°时，若函数值y＞0，求对应自变量x的取值范围；
（Ⅲ）无论m取何值，该抛物线都经过定点H．当∠AHP＝45°时，求抛物线的解析式．
【答案】（Ⅰ）顶点P（﹣
，﹣
）；（Ⅱ）当函数值y＞0，对应自变量x的取值范围为x＜5﹣
或x＞5+；（Ⅲ）抛物线解析式为y＝x2﹣
x+
或y＝x2﹣
x+
．
【解析】
（Ⅰ）把点A代入抛物线解析式求得m，将抛物线配方成顶点式即求得P的坐标．
（Ⅱ）由点P在x轴下方，当∠AOP＝45°得点P在直线y＝x上．把抛物线配方得用m表示的点P坐标，代入y＝x即求得m的值．令抛物线y＝0解方程求得抛物线与x轴两交点坐标，由图象可知，在抛物线两侧有函数值y＞0，即得到x的取值范围．
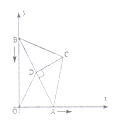
（Ⅲ）发现当x＝2时，y＝4，所以定点H（2，4）．过点AA作AB⊥PH于点B，过点B作DC⊥x轴于点C，过点H作HD⊥CD于点D，构造△ABC≌△BHD，利用对应边AC＝BD，BC＝HD求点B坐标，再求直线BH解析式，把点用m表示的点P坐标代入BH解析式即求得m的值．由于满足∠AHP＝45°的点P可以在AH左侧或右侧，故需分情况讨论．
（Ⅰ）把A（1，0）代入y＝x2+mx﹣2m得：
1+m﹣2m＝0，解得：m＝1
∴抛物线解析式为y＝x2+x﹣2＝（x+）2﹣
∴顶点P（﹣，﹣），
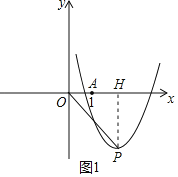
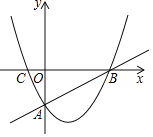
（Ⅱ）过P作PH⊥x轴于点H，如图1
∵点P在x轴下方且∠AOP＝45°
∴△POH是等腰直角三角形，P在第四象限
∴OH＝PH，
∵y＝x2+mx﹣2m＝（x+
）2﹣
﹣2m
∴P（﹣，﹣
﹣2m）（m＜0）
∴﹣＝+2m
解得：m1＝0（舍去），m2＝﹣10
∴抛物线解析式为y＝x2﹣10x+20
当y＝0时，解得：x1＝5﹣，x2＝5+
由图象可知，当函数值y＞0，对应自变量x的取值范围为x＜5﹣或x＞5+．
（Ⅲ）当x＝2时，y＝4+2m﹣2m＝4
∴无论m取何值，该抛物线都经过定点H（2，4）
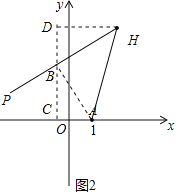
过点A作AB⊥PH于点B，过点B作DC⊥x轴于点C，过点H作HD⊥CD于点D，
∴∠ABH＝∠ACB＝∠BDH＝90°
∴∠ABC+∠DBH＝∠ABC+∠BAC＝90°
∴∠BAC＝∠DBH
∵∠AHP＝45°
∴△ABH是等腰直角三角形，AB＝BH
在△ABC与△BHD中
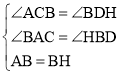
∴△ABC≌△BHD（AAS）
∴AC＝BD，BC＝HD
设点B坐标为（a，b）
①若点P在AH左侧，即点B在AH左侧，如图2
∴AC＝1﹣a，BC＝b，BD＝4﹣b，DH＝2﹣a
∴
解得：
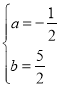
∴点B（﹣，
）
设直线BH解析式为y＝kx+h
∴
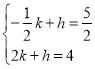解得：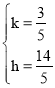
∴直线BH：y＝
x+
∵点P（﹣，﹣
﹣2m）在直线BH上
∴（﹣）+＝﹣﹣2m
解得：m1＝﹣，m2＝﹣4
∵m＝﹣4时，P（2，4）与点H重合，要舍去
∴抛物线解析式为y＝x2﹣x+，
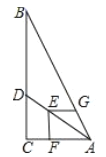
②若点P在AH右侧，即点B在AH右侧，如图3
∴AC＝a﹣1，BC＝b，BD＝4﹣b，DH＝a﹣2
∴
解得：
∴点B（
，
）
设直线BH解析式为y＝kx+h
∴
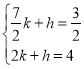解得：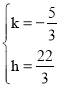
∴直线BH：y＝﹣
x+
∵点P（﹣，﹣﹣2m）在直线BH上
∴﹣×（﹣）+＝﹣﹣2m
解得：m1＝﹣，m2＝﹣4（舍去）
∴抛物线解析式为y＝x2﹣x+
综上所述，抛物线解析式为y＝x2﹣x+或y＝x2﹣x+.
