题目内容
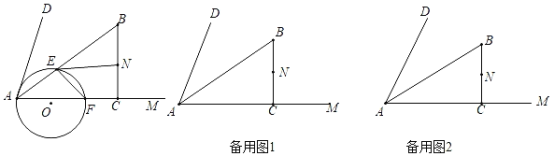
【题目】在△ABC中,∠BAC=60°,AD平分∠BAC交边BC于点D,分别过D作DE∥AC交边AB于点E,DF∥AB交边AC于点F.
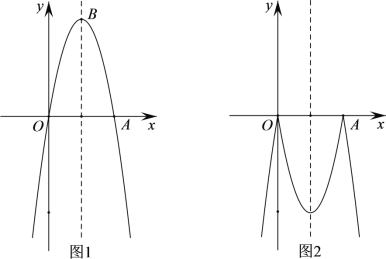
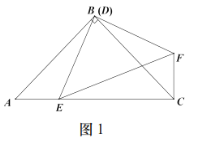
(1)如图1,试判断四边形AEDF的形状,并说明理由;
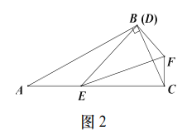
(2)如图2,若AD=4![]() ,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.
,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.
(i)求ENEG的值;
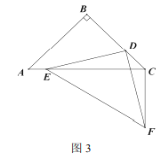
(ii)将线段DM绕点D顺时针旋转60°得到线段DM′,求证:H,F,M′三点在同一条直线上
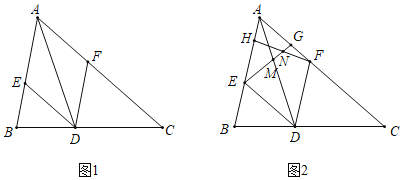
【答案】(1) 四边形AEDF的形状是菱形,理由见解析;(1) (i) 12;(ii)见解析
【解析】
(1)由题意得出四边形AEDF是平行四边形;再根据角平分线性质及平行线性质可推出∠EAD=∠EDA;根据等角对等边得出AE=DE即可得出;
(2) (i) 连接EF交AD于点Q,根据菱形的性质得出△AEF是等边三角形,再根据余弦得出AE=AF=EF=4,根据SAS得出△AEG≌△EFH,根据全等三角形性质得出△AEG∽△NEH,最后根据相似三角形的性质得出答案;
(ii) 连接FM',根据等边三角形的性质及旋转的性质可得出△EDM≌△FDM',再根据全等三角形性质、等量代换即可得出答案.
(1)解:四边形AEDF的形状是菱形;理由如下:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∵AD平分∠BAC,
∴∠EAD=∠FAD,
∵DE∥AC,
∴∠EDA=∠FAD,
∴∠EAD=∠EDA,
∴AE=DE,
∴四边形AEDF是菱形;
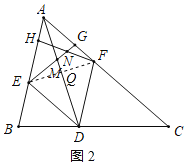
(2)(i)解:连接EF交AD于点Q,如图2所示:
∵∠BAC=60°,四边形AEDF是菱形,
∴∠EAD=30°,AD、EF相互垂直平分,△AEF是等边三角形,
∴∠EAF=∠AEF=∠AFE=60°,
∵AD=![]() ,
,
∴AQ=![]() ,
,
在Rt△AQE中,cos∠EAQ=![]() ,即cos30°=
,即cos30°=![]() ,
,
∴AE=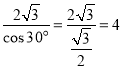 ,
,
∴AE=AF=EF=4,
在△AEG和△EFH中, ,
,
∴△AEG≌△EFH(SAS),
∴∠AEG=∠EFH,
∴∠ENH=∠EFH+∠GEF=∠AEG+∠GEF=60°,
∴∠ENH=∠EAG,
∵∠AEG=∠NEH,
∴△AEG∽△NEH,
∴![]() ,
,
∴ENEG=EHAE=3×4=12;
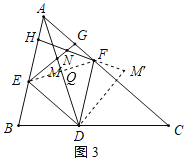
(ii)证明:如图3,连接FM',
∵DE∥AC,
∴∠AED=180°﹣∠BAC=120°,
由(1)得:△EDF是等边三角形,
∴DE=DF,∠EDF=∠FED=∠EFD=60°,
由旋转的性质得:∠MDM'=60°,DM=DM',
∴∠EDM=∠FDM',
在△EDM和△FDM'中,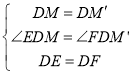 ,
,
∴△EDM≌△FDM'(SAS),
∴∠MED=∠DFM',
由(i)知,∠AEG=∠EFH,
∴∠DFM'+∠EFH=∠MED+∠AEG=∠AED=120°,
∴∠HFM'=∠DFM'+∠HFE+∠EFD=120°+60°=180°,
∴H,F,M′三点在同一条直线上.

 名校课堂系列答案
名校课堂系列答案