题目内容
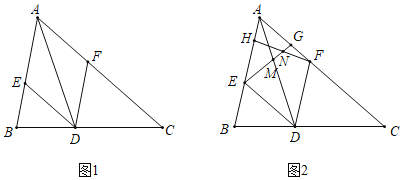
【题目】如图,正方形ABCD中,点E为对角线AC上一点,且AE![]() CB,连接DE并延长交BC于点G,过点A作AH⊥BE于点H,交BC于点F.以下结论:①BH
CB,连接DE并延长交BC于点G,过点A作AH⊥BE于点H,交BC于点F.以下结论:①BH![]() HE;②∠BEG
HE;②∠BEG![]() 45°;③△ABF ≌△DCG; ④4BH2
45°;③△ABF ≌△DCG; ④4BH2![]() BG·CD.其中正确结论的个数是( )
BG·CD.其中正确结论的个数是( )
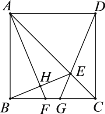
A.1个B.2
C.3D.4
【答案】D
【解析】
利用正方形的性质得到AB=BC=AE,由此得到判断①正确;先求出∠BAC=∠DAC=45°,利用等腰三角形的性质求出∠AEB=∠AED=![]() ,再根据对顶角相等及平角求出∠BEG,由此判断②;根据等腰三角形的三线合一的性质求出∠BAF=
,再根据对顶角相等及平角求出∠BEG,由此判断②;根据等腰三角形的三线合一的性质求出∠BAF=![]() ,推出∠DGC=∠AFB
,推出∠DGC=∠AFB![]() ,即可判断③;证明△BEG∽△DCE,即可判断④.
,即可判断③;证明△BEG∽△DCE,即可判断④.
∵四边形ABCD是正方形,
∴AB=BC,
∵AE=CB,
∴AE=AB,
∵AH⊥BE,
∴BH=HE,即①正确;
∵AC是正方形ABCD的对角线,
∴∠BAC=∠DAC=45°,
∵AE=AB=AD,
∴∠AEB=∠AED=![]() ,
,
∴∠CEG=∠AED=67.5°,
∴∠BEG=180°-∠AEB-∠CEG=45°,故②正确;
∵AB=AE,AH⊥BE,
∴∠BAF=![]()
∵![]()
∴![]()
∵AD∥BC,
∴∠DGC=∠ADE![]()
∴∠AFB=∠DGC,
又∵AB=DC,∠DCG=![]()
∴△ABF ≌△DCG,故③正确;
∵BC=DC,∠BCE=∠DCE=45°,CE=CE,
∴△BCE≌△DCE,
∴BE=DE,∠CBE=∠CDE,
∵∠BEG=∠DCE=45°,
∴△BEG∽△DCE,
∴![]()
∴![]() ,
,
∵DE=BE=2BH,
∴4BH2![]() BG·CD,故④正确,
BG·CD,故④正确,
故正确的有①②③④,
故选:D.

 桃李文化快乐暑假武汉出版社系列答案
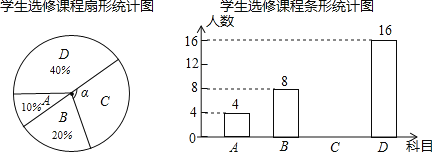
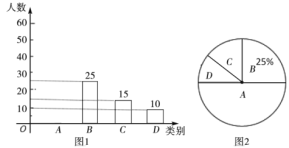
桃李文化快乐暑假武汉出版社系列答案【题目】面对疫情,每个人都需要积极行动起来,做好预防工作.为此某校开展了“新型冠状病毒肺炎”防控知识竞赛.现从该校五、六年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用![]() 表示,共分成四组:A.
表示,共分成四组:A.![]() ,B.
,B.![]() ,C.
,C.![]() ,D.
,D.![]() ),下面给出了部分信息:
),下面给出了部分信息:
五年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
六年级10名学生的竞赛成绩在C组中的数据是:94,90,94
五、六年级抽取的学生竞赛成绩统计表
年级 | 平均数 | 中位数 | 众数 | 方差 |
五年级 | 92 | 93 |
| 52 |
六年级 | 92 |
| 100 | 50.4 |
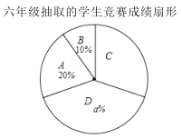
是据以上信息,解答下列问题:
(1)直接写出上述图表中![]() ,
,![]() ,
,![]() 的值:
的值:![]() __________,
__________,![]() ___________,
___________,![]() ___________;
___________;
(2)由以上数据,你认为该校五、六年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校五、六年级共1800人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀![]() 的学生人数是多少?
的学生人数是多少?
【题目】受“新冠”疫情的影响,某销售商在网上销售![]() 、
、![]() 两种型号的“手写板”,获利颇丰.已知
两种型号的“手写板”,获利颇丰.已知![]() 型,
型,![]() 型手写板进价、售价和每日销量如表格所示:
型手写板进价、售价和每日销量如表格所示:
进价(元/个) | 售价(元/个) | 销量(个/日) | |
|
|
|
|
|
|
|
|
根据市场行情,该销售商对![]() 型手写板降价销售,同时对
型手写板降价销售,同时对![]() 型手写板提高售价,此时发现
型手写板提高售价,此时发现![]() 型手写板每降低
型手写板每降低![]() 元就可多卖
元就可多卖![]() 个,
个,![]() 型手写板每提高
型手写板每提高![]() 元就少卖
元就少卖![]() 个,要保持每天销售总量不变,设其中
个,要保持每天销售总量不变,设其中![]() 型手写板每天多销售
型手写板每天多销售![]() 个,每天总获利的利润为
个,每天总获利的利润为![]() 元
元
(1)求![]() 与
与![]() 之间的函数关系式并写出
之间的函数关系式并写出![]() 的取值范围;
的取值范围;
(2)要使每天的利润不低于![]() 元,直接写出
元,直接写出![]() 的取值范围;
的取值范围;
(3)该销售商决定每销售一个![]() 型手写板,就捐
型手写板,就捐![]() 元给
元给![]() 因“新冠疫情”影响的困难家庭,当
因“新冠疫情”影响的困难家庭,当![]() 时,每天的最大利润为
时,每天的最大利润为![]() 元,求
元,求![]() 的值.
的值.