题目内容
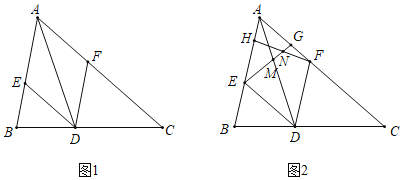
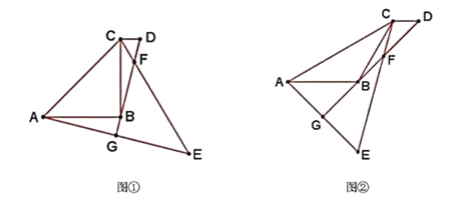
【题目】已知![]() 中
中![]() 点
点![]() 分别在边
分别在边![]() 、边
、边![]() 上,连接
上,连接![]() 点
点![]() 、点
、点![]() 在直线
在直线![]() 同侧,连接
同侧,连接![]() 且
且![]() .
.
(1)点![]() 与点
与点![]() 重合时,
重合时,
①如图1,![]() 时,
时,![]() 和
和![]() 的数量关系是 ;位置关系是 ;
的数量关系是 ;位置关系是 ;
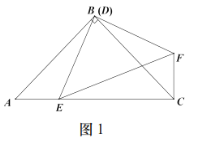
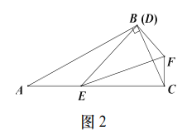
②如图2,![]() 时,猜想
时,猜想![]() 和
和![]() 的关系,并说明理由;
的关系,并说明理由;
(2)![]() 时,
时,
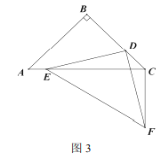
③如图3,![]() 时,若
时,若![]() 求
求![]() 的长度;
的长度;
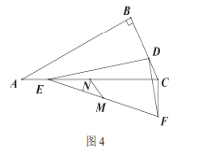
④如图4,![]() 时,点
时,点![]() 分别为
分别为![]() 和
和![]() 的中点,若
的中点,若![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
【答案】(1)①AE=FC;AE⊥FC;②AE=2FC;AE⊥FC;理由见解析;(2)③FC = 6;④MN的最小值为![]() .
.
【解析】
(1)①利用SAS证出△ABE≌△CDF,从而证出AE=FC,∠A=∠DCF,然后证出∠ACF=90°即可得出结论;
②根据相似三角形的判定证出△ABE∽△CDF,从而得出∠A=∠DCF,![]() ,然后证出∠ACF=90°即可得出结论;
,然后证出∠ACF=90°即可得出结论;
(2)③作GD⊥BC于点D,交AC于点G;作GH⊥AB于点H,交AB于点H;DM⊥AC,利用SAS证出△EDG≌△FDC,从而得出EG=FC,令DC=a,BD=2a,根据三角形的面积公式即可求出a值,从而求出结论;
④连接MD和MC,根据直角三角形斜边上的中线等于斜边的一半可得DM=CM=![]() ,从而得出点M的运动轨迹为是CD的垂直平分线的一部分,作CD的垂直平分线MH交BC于H,然后证出四边形NMHG为平行四边形,从而求出结论.
,从而得出点M的运动轨迹为是CD的垂直平分线的一部分,作CD的垂直平分线MH交BC于H,然后证出四边形NMHG为平行四边形,从而求出结论.
(1)①解:∵![]()
![]()
∴∠ABC=∠EDF=90°,∠A+∠BCA=90°
∴∠ABE+∠EDC=∠CDF+∠EDC
∴∠ABE=∠CDF
∵![]()
∴AB=CB,DE=DF
∴△ABE≌△CDF
∴AE=FC,∠A=∠DCF
∴∠DCF+∠BCA=90°
∴∠ACF=90°
∴AE⊥FC
故答案为:AE=FC;AE⊥FC;
②证明:AE=2FC;AE⊥FC
∵DF⊥DE
∴∠EDF=∠ABC=90°
∴∠ABE=∠CDF·
∵![]()
∴△ABE∽△CDF
∴∠A=∠DCF,![]()
∵∠A+∠ACB=90°
∴∠DCF+∠ACB=90°
∴∠ACF=90°;即FC⊥AE·
(2)③解:作GD⊥BC于点D,交AC于点G;作GH⊥AB于点H,交AB于点H;DM⊥AC.
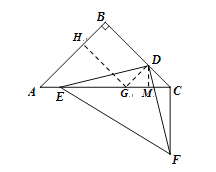
∴四边形BDGH为矩形
∴DB=HG
∵∠ABC=90°,![]()
∴∠A=∠HGA =∠ACB=45°
∴DC=DG
∵DE⊥DF
∴∠EDG=∠FDC
∴△EDG≌△FDC(SAS)
∴EG=FC
∵BD=2CD
∴令DC=a,BD=2a
∴AG=![]()
∴EG=![]() ,MD=
,MD=![]() ·
·
∵![]()
∴![]()
解得![]() ,
,![]() (舍)
(舍)
∴FC = EG=6
④∵![]() ,AB=10
,AB=10
∴BC=5
∵![]()
∴CD=![]()
![]()
由③易证∠ECF=90°
在Rt△EDF和Rt△ECF中,点M为EF的中点,连接MD和MC
∴DM=CM=![]()
∴点M的运动轨迹为是CD的垂直平分线的一部分,作CD的垂直平分线MH交BC于H
∴当NM⊥MH时,MN的最小,易知MN∥BC,MH∥AB,CH=![]() =
=![]()
取BC的中点G,连接NG,则CG=![]() =
=![]()
∴NG为△ABC的中位线
∴NG∥AB
∴MH∥NG
∴四边形NMHG为平行四边形
∴此时MN=GH=CG-CH=![]()
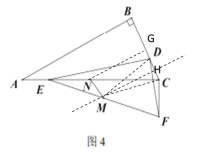
即MN的最小值为![]() .
.

【题目】受“新冠”疫情的影响,某销售商在网上销售![]() 、
、![]() 两种型号的“手写板”,获利颇丰.已知
两种型号的“手写板”,获利颇丰.已知![]() 型,
型,![]() 型手写板进价、售价和每日销量如表格所示:
型手写板进价、售价和每日销量如表格所示:
进价(元/个) | 售价(元/个) | 销量(个/日) | |
|
|
|
|
|
|
|
|
根据市场行情,该销售商对![]() 型手写板降价销售,同时对
型手写板降价销售,同时对![]() 型手写板提高售价,此时发现
型手写板提高售价,此时发现![]() 型手写板每降低
型手写板每降低![]() 元就可多卖
元就可多卖![]() 个,
个,![]() 型手写板每提高
型手写板每提高![]() 元就少卖
元就少卖![]() 个,要保持每天销售总量不变,设其中
个,要保持每天销售总量不变,设其中![]() 型手写板每天多销售
型手写板每天多销售![]() 个,每天总获利的利润为
个,每天总获利的利润为![]() 元
元
(1)求![]() 与
与![]() 之间的函数关系式并写出
之间的函数关系式并写出![]() 的取值范围;
的取值范围;
(2)要使每天的利润不低于![]() 元,直接写出
元,直接写出![]() 的取值范围;
的取值范围;
(3)该销售商决定每销售一个![]() 型手写板,就捐
型手写板,就捐![]() 元给
元给![]() 因“新冠疫情”影响的困难家庭,当
因“新冠疫情”影响的困难家庭,当![]() 时,每天的最大利润为
时,每天的最大利润为![]() 元,求
元,求![]() 的值.
的值.