��Ŀ����
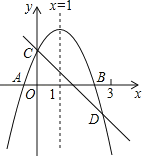
����Ŀ����ͼ1����֪������C1��![]() ��x��������ύ�ڵ�A����BΪ�����ߵĶ��㣬ֱ��l��
��x��������ύ�ڵ�A����BΪ�����ߵĶ��㣬ֱ��l��![]() ��һ����ֱ�ߣ�
��һ����ֱ�ߣ�
(1)���A����B�����ꣻ
(2)��ֱ��l������Aʱ�����ֱ��l�Ľ���ʽ����ֱ��д����ʱ��![]() ʱ���Ա���x��ȡֵ��Χ��
ʱ���Ա���x��ȡֵ��Χ��
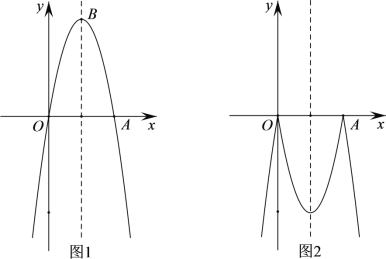
(3)��ͼ2����������C1��x���Ϸ��IJ�����x�ᷭ�ۣ���C1��x���·���ͼ����ϳ�һ���µ�ͼ��C2����ֱ��l�����ͼ��C2����ֻ����������ʱ��ֱ��д��k��ȡֵ��Χ��
���𰸡�(1)A(2, 0)��B(1��3)��(2)x>2��x<![]() ��(3)
��(3)![]() ��k<0
��k<0
��������
��1����ʽ�������A��B�����ꣻ
��2��A�����ֱ�ߣ�����������ʽ������y1��y2�������ֱ�߽���ʽ�����ͼ����÷���Ҫ���x��ȡֵ��Χ��
��3�����ͼ��۲죬![]() ��k<0ʱ��ֻ����������.
��k<0ʱ��ֻ����������.
(1)��y=0��![]() ��
��
��ã�![]()
![]() ��
��
��A(2, 0)��
��![]() ��
��
��x=1ʱ��y=3��
��B(1��3)
(2)��A(2��0)����![]() ��
�У�![]()
��ֱ�߽���ʽΪ��![]() ��
��
����������������ͼ����һ����Ϊ��-![]() ��-
��-![]() ����
����
���ͼ��![]() ʱ��
ʱ��
x>2��x<![]() ��
��
(3)��ͼ���֪����ֱ�߾���A��ʱ��ǡ���������㣬
��ֱ�������˶�ʱ��ֻ���������㣬
��![]() ʱ��ǡ���������㣻
ʱ��ǡ���������㣻
��k<0ʱ���������������㣬����������
��![]() ��k<0.
��k<0.

 �ŵ������ϵ�д�
�ŵ������ϵ�д�