��Ŀ����
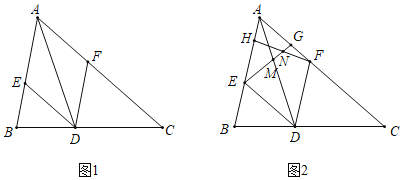
����Ŀ����ͼ������DAM�ڲ���Rt��ABC��ABƽ����DAM����ACB��90����AB��10��AC��8����NΪBC���е㣬����E��A���������AB�˶����ٶ�Ϊÿ��5����λ������F��A���������AM�˶����ٶ�Ϊÿ��8����λ������E�����Bʱ������ͬʱֹͣ�˶�����A��E��F����O��
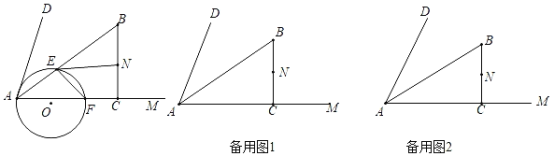
��1���ж���AEF����״Ϊ�� �������ж�AD����O��λ�ù�ϵΪ�� ����
��2����tΪ��ֵʱ��EN����O���У������ʱ��O�İ뾶�����Ƚϰ뾶���ӻ�![]() ���ȵĴ�С��
���ȵĴ�С��
��3��ֱ��д����AEF�������˶���·����Ϊ�� ������ע����A��E��F�غ�ʱ�����ľ���A�㣩
��4��ֱ��д���߶�EN����O������������ʱ��t��ȡֵ��ΧΪ�� ����
���ο����ݣ�sin37����![]() ��tan37����
��tan37����![]() ��tan74���
��tan74���![]() ��sin74���
��sin74���![]() ��cos74���
��cos74���![]() ��
��
���𰸡���1�����������Σ����У���2��t=1���뾶Ϊ![]() ���ӻ�
���ӻ�![]() ���ȴ��ڰ뾶����3��
���ȴ��ڰ뾶����3��![]() ����4��1��t��
����4��1��t��![]()
��������
��1������E��EH��AF��H������OA��OE��OH���ɹ��ɶ������BC��![]() ��6�����˶�ʱ��Ϊt����AE��5t��AF��8t��֤����EAH�ס�BAC���ó�
��6�����˶�ʱ��Ϊt����AE��5t��AF��8t��֤����EAH�ס�BAC���ó�![]() �����AH��4t����FH��AF��AH��4t��AH��FH���ó���AEF�ǵ��������Σ�֤��E��H��O���㹲�ߣ��ó���OAF+��AOE��90������ABƽ����DAM���ó���DAE����EAF����EFA����Բ�ܽǶ����ó���AOE��2��EFA������DAF+��OAF��90������DAO����OA��AD�����ɵó�AD����O���У�
�����AH��4t����FH��AF��AH��4t��AH��FH���ó���AEF�ǵ��������Σ�֤��E��H��O���㹲�ߣ��ó���OAF+��AOE��90������ABƽ����DAM���ó���DAE����EAF����EFA����Բ�ܽǶ����ó���AOE��2��EFA������DAF+��OAF��90������DAO����OA��AD�����ɵó�AD����O���У�
��2������OA��OF��OE��OE��AC����H����֤�ı���EHCNΪ���Σ��ó�EH��NC���ɹ��ɶ����ó�EH��![]() ��3t����NC��3t��BC��2NC��6t����BC��6���ó�t��1����AH��4��EH��3������O�İ뾶Ϊx����OH��x��3���ɹ��ɶ����ó�OA2��OH2+AH2�����x��
��3t����NC��3t��BC��2NC��6t����BC��6���ó�t��1����AH��4��EH��3������O�İ뾶Ϊx����OH��x��3���ɹ��ɶ����ó�OA2��OH2+AH2�����x��![]() ���ó�OH��
���ó�OH��![]() ��tan��AOH��
��tan��AOH��![]() ���ó���AOH��74��������AOH��60��ʱ����AOE�ǵȱ������Σ�AE��OA��74����60�����ó�AE��OA�����ӻ�
���ó���AOH��74��������AOH��60��ʱ����AOE�ǵȱ������Σ�AE��OA��74����60�����ó�AE��OA�����ӻ�![]() ���ȵĴ��ڰ뾶��
���ȵĴ��ڰ뾶��
��3������E�˶���B��ʱ��t��2��AF��16��AE��EF��AB��10����ʱ��AEF�����ļ�ΪG����A��E��F�غ�ʱ������ΪA�㣬��AEF�������˶���·����ΪAG����GP��AE��P��GQ��EF��Q������AG��GF����CG��PG��NQ��S��AEF��![]() AFBC��48����CG��PG��NQ��a����S��AEF��S��AGF+S��AEB+S��FEG��
AFBC��48����CG��PG��NQ��a����S��AEF��S��AGF+S��AEB+S��FEG��![]() AFCG+
AFCG+![]() AEPG+
AEPG+![]() EFNQ��
EFNQ��![]() ��(16+10+10)a��48�����a��
��(16+10+10)a��48�����a��![]() ���ɹ��ɶ����ó�AC2+CG2��AG2���ó�AG��
���ɹ��ɶ����ó�AC2+CG2��AG2���ó�AG��![]() ��
��
��4���ֱ��������ּ���λ�ã�����EN����O����ʱ���ɣ�2��֪��t��1������N����O�ϣ���ONΪ��O�İ뾶������OA��ON��OE��OE��AC��H������O��OK��BC��K�����ı���OKCHΪ���Σ�OA��OE��ON���ó�OH��CK��AH��4t��EH��3t������O�İ뾶Ϊx���ɹ��ɶ����ó�AH2+OH2��OA2�����x��![]() t����OH��CK��
t����OH��CK��![]() t���ɹ��ɶ����ó�
t���ɹ��ɶ����ó�![]() �����t��
�����t��![]() �����ɵó������
�����ɵó������
��1������E��EH��AF��H������OA��OE��OH����ͼ1��ʾ��
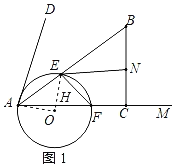
�ߡ�ACB��90����AB��10��AC��8��
��BC��![]() ��6��
��6��
���˶�ʱ��Ϊt����AE��5t��AF��8t��
�ߡ�AHE����ACB��90������EAH����BAC��
���EAH�ס�BAC��
��![]() ����
����![]() ��
��
��AH��4t��
��FH��AF��AH��8t��4t��4t��
��AH��FH��
��EH��AF��
���AEF�ǵ��������Σ�
��EΪ![]() ���е㣬��EAF����EFA��
���е㣬��EAF����EFA��
��AH��FH��
��OH��AC��
��E��H��O���㹲�ߣ�
���OAF+��AOE��90����
��ABƽ����DAM��
���DAE����EAF����EFA��
�ߡ�AOE��2��EFA��
���AOE����DAE+��EAF����DAF��
���DAF+��OAF��90������DAO����OA��AD��
��OAΪ��O�İ뾶��
��AD����O����
�ʴ�Ϊ�����������Σ����У�
��2������OA
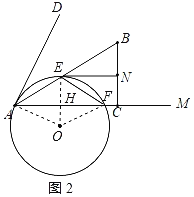
�ɣ�1��֪��EH��AC��
��EN����O����
���OEN��90����
�ߡ�ACB��90����
���ı���EHCNΪ���Σ�
��EH��NC��
��Rt��AHE��EH��![]() ��3t��
��3t��
��NC��3t��
����NΪBC���е㣬
��BC��2NC��6t��
��BC��6��
��6t��6��
��t��1��
��AH��4��EH��3��
����O�İ뾶Ϊx����OH��x��3��
��Rt��AOH�У��ɹ��ɶ����ã�OA2��OH2+AH2����x2��(x��3)2+42��
��ã�x��![]() ��
��
���O�İ뾶Ϊ![]() ��
��
��OH��![]() ��
��
��tan��AOH��![]() ��
��![]() ��
��
���AOH��74����
�ߡ�AOH��60��ʱ����AOE�ǵȱ������Σ�AE��OA��74����60����
��AE��OA��
���ӻ�![]() ���ȵĴ��ڰ뾶��
���ȵĴ��ڰ뾶��
��3������E�˶���B��ʱ��t��10��5��2��
��AF��2��8��16��AE��EF��AB��10��
��ʱ��AEF�����ļ�ΪG����A��E��F�غ�ʱ������ΪA�㣬
���AEF�������˶���·����ΪAG��
��GP��AE��P��GQ��EF��Q������AG��GF����CG��PG��NQ����ͼ3��ʾ��
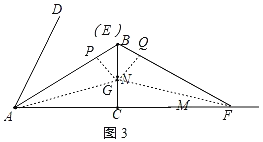
S��AEF��![]() AFBC��
AFBC��![]() ��16��6��48��
��16��6��48��
��CG��PG��NQ��a��
��S��AEF��S��AGF+S��AEB+S��FEG��![]() AFCG+
AFCG+![]() AEPG+
AEPG+![]() EFNQ��
EFNQ��![]() ��(16+10+10)a��48��
��(16+10+10)a��48��
��ã�a��![]() ��
��
��Rt��AGC��AC2+CG2��AG2����82+(![]() )2��AG��
)2��AG��
��AG��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��4���ֱ��������ּ���λ�ã�
����EN����O����ʱ���ɣ�2��֪��t��1��
����N����O�ϣ���ONΪ��O�İ뾶��
����OA��ON��OE��OE��AC��H������O��OK��BC��K����ͼ4��ʾ��
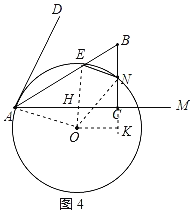
���ı���OKCHΪ���Σ�OA��OE��ON��
��OH��CK��AH��4t��EH��3t��
����O�İ뾶Ϊx��
����Rt��AOH��AH2+OH2��OA2����(4t)2+(x��3t)2��x2��
��ã�x��![]() t��
t��
��OH��CK��![]() t��3t��
t��3t��![]() t��
t��
��Rt��OKN��OK2+KN2��ON2����(8��4t)2+(3+![]() t)2��(
t)2��(![]() t)2��
t)2��
��ã�t��![]() ��
��
���߶�EN����O������������ʱ��t��ȡֵ��ΧΪ��1��t��![]() ��
��
�ʴ�Ϊ��1��t��![]() ��
��

 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�