题目内容
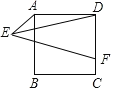
【题目】如图,△ABC内接于⊙O,AB为⊙O的直径,D为![]() 的中点,过D作DF⊥AB于点E,交⊙O于点F,交弦BC于点G,连接CD,BF.
的中点,过D作DF⊥AB于点E,交⊙O于点F,交弦BC于点G,连接CD,BF.
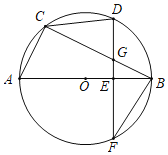
(1)求证:△BFG≌△DCG;
(2)若AC=10,BE=8,求BF的长;
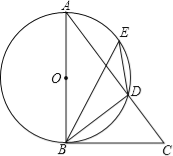
(3)在(2)的条件下,P为⊙O上一点,连接BP,CP,弦CP交直径AB于点H,若△BPH与△CPB相似,求CP的长.
【答案】(1)见解析;(2)BF=4![]() ;(3)PC=17
;(3)PC=17![]() .
.
【解析】
(1)证明BF=CD,而∠BFG=∠DCG,∠BGF=∠DGC,则△BFG≌△DCG(AAS);
(2)证明OM是△ABC的中位线,进而在Rt△BEF中,利用勾股定理求解即可;
(3)证明∠ACP=∠BCP=45°,在Rt△CBN中,CN=BN=![]() BC=12
BC=12![]() ,而∠CAB=∠CPB,则tan∠CAB=tan∠CPB,即可求解.
,而∠CAB=∠CPB,则tan∠CAB=tan∠CPB,即可求解.
(1)∵D是![]() 的中点,则
的中点,则![]() =
=![]() ,
,
∵AB为⊙O的直径,DF⊥AB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BF=CD,
又∵∠BFG=∠DCG,∠BGF=∠DGC,
∴△BFG≌△DCG(AAS);
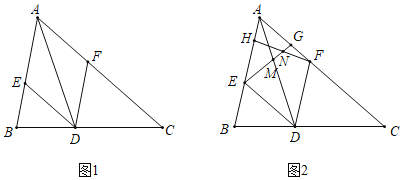
(2)如图1,连接OD交BC于点M,
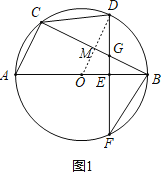
∵D为![]() 的中点,
的中点,
∴OD⊥BC,∴BM=CM,
∵OA=OB,
∴OM是△ABC的中位线,
∴OM=![]() AC=5,
AC=5,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴OE=OM=5,
∴OD=OB=OE+BE=5+8=13,
∴EF=DE=![]() =12,
=12,
∴BF=![]() =4
=4![]() ;
;
(3)如图2,
∵弦CP交AB于点H,则点P与点C在直径的两侧,则∠CBP>∠HBP,
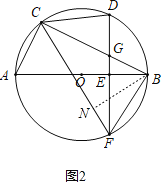
又∵∠CPB=∠BPH,
∴∠ACP=∠BCP,
∵AB是直径,则∠ACB=∠APB=90°,
∴∠ACP=∠BCP=45°,
过点B作BN⊥PC于点N,由(2)得AB=26,
在Rt△CBN中,CN=BN=![]() BC=12
BC=12![]() ,
,
∵∠CAB=∠CPB,
∴tan∠CAB=tan∠CPB=![]() ,即
,即![]() =
=![]() ,故PN=5
,故PN=5![]() ,
,
∴PC=CN+PN=5![]() +12
+12![]() =17
=17![]() .
.

 特高级教师点拨系列答案
特高级教师点拨系列答案