题目内容
【题目】已知矩形ABCD中,若AB=4,BC=2,点E为CD的中点,F为AB上一点,连接EF、DF,EF=![]() ,则DF=_____.
,则DF=_____.
【答案】![]() 或
或![]()
【解析】
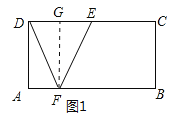
分两种情况:①点F靠近点A时,如图1,作FG⊥CD于G,则FG=BC=2,∠FGE=90°,由勾股定理可求出GE,由矩形的性质和已知条件可得DG,再根据勾股定理即可求出DF的长;②点F靠近点B时,如图2,同①的方法得出EG和DG的长,再根据勾股定理求出DF的长即可.
解:分两种情况:
①点F靠近点A时,如图1所示:作FG⊥CD于G,则FG=BC=2,∠FGE=90°,
∴GE=![]() =1,
=1,
∵四边形ABCD是矩形,∴CD=AB=4,
∵E是CD的中点,∴DE=![]() CD=2,∴DG=2﹣1=1,
CD=2,∴DG=2﹣1=1,
∴DF=![]() ;
;
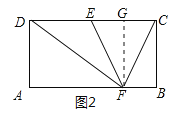
②点F靠近点B时,如图2所示:作FG⊥CD于G,则FG=BC=2,∠FGE=90°,同①得出EG=1,∴DG=DE+EG=3,
∴DF=![]() ;
;
综上所述:DF的长为![]() 或
或![]() ;
;
故答案为:![]() 或
或![]() .
.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目