题目内容
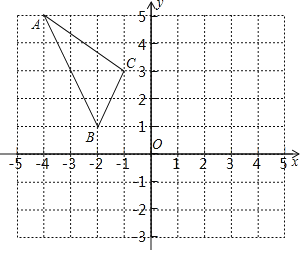
【题目】已知一次函数![]() 的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数
的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数![]() (k≠0)图象在第二象限内的交点.
(k≠0)图象在第二象限内的交点.
(1)求点B的坐标及k的值;
(2)试在x轴上确定点C,使AC=AB,请直接写出点C的坐标.
【答案】(1)B(-l,3),k=-3;(2)(2,0),(-2,0).
【解析】
(1)由点B的横坐标利用一次函数图象上点的坐标特征即可求出点B的坐标,根据点B的坐标利用反比例函数图象上点的坐标特征即可求出k值;
(2)令x=0利用一次函数图象上点的坐标特征可求出点A的坐标,设点C的坐标为(m,0),根据两点间的距离公式结合AC=AB即可得出关于m的方程,解之即可得出m的值,进而得出点C的坐标.
(1)∵点B(-1,n)在直线y=-2x+1上,
∴n=2+1=3.
∴点B的坐标为(-1,3).
∵点B(-1,3)在反比例函数y=![]() 的图象上,
的图象上,
∴k=-3.
(2)当x=0时,y=-2x+1=1,
∴点A的坐标为(0,1).
设点C的坐标为(m,0),
∵AC=AB,
∴![]() ,
,
解得:m=±2.
∴点C的坐标为(2,0)或(-2,0).

练习册系列答案
相关题目
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为200人 B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选F的人数为35人 D. 被调查的学生中最想选D的有55人