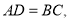题目内容
【题目】如图,在网格纸中,![]() 、
、![]() 都是格点,以
都是格点,以![]() 为圆心,
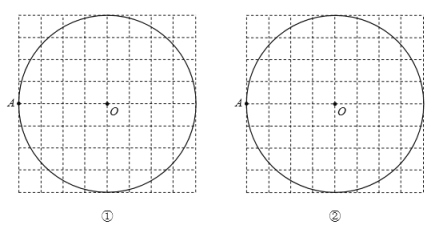
为圆心,![]() 为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
(1)在圆①中画圆![]() 的一个内接正六边形
的一个内接正六边形![]() ;
;
(2)在图②中画圆![]() 的一个内接正八边形
的一个内接正八边形![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)设AO的延长线与圆交于点D,根据正六边形的性质,点D即为正六边形的一个顶点,且正六边形的边长等于圆的半径,根据垂直平分线的性质即可确定其它的顶点;
(2)先求出内接八边形的中心角,然后根据正方形的性质即可找到各个顶点.
(1)设AO的延长线与圆交于点D,
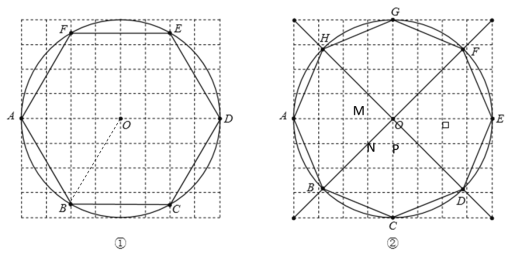
根据圆的内接正六边形的性质,点D即为正六边形的一个顶点,且正六边形的边长等于圆的半径,即OB=AB,故在图中找到AO的中垂线与圆的交点即为正六边形的顶点B和F;同理:在图中找到OD的中垂线与圆的交点即为正六边形的顶点C和E,连接AB、BC、CD、DE、EF、FA,如图①,正六边形![]() 即为所求.
即为所求.
(2)圆的内接八边形的中心角为360°÷8=45°,而正方形的对角线与边的夹角也为45°
∴在如②图所示的正方形OMNP中,连接对角线ON并延长,交圆于点B,此时∠AON=45°;∵∠NOP=45°,
∴OP的延长线与圆的交点即为点C
同理,即可确定点D、E、F、G、H的位置,顺次连接,
如图②,正八边形![]() 即为所求.
即为所求.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
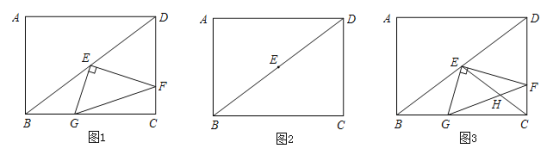
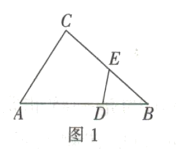
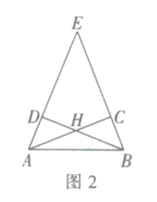
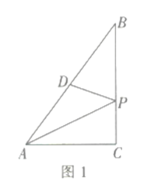
小学生10分钟应用题系列答案【题目】如图1,在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() .若
.若![]() 设
设 ![]() (当点
(当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值为
的值为![]() ),
),![]() .
.
小明根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.
![]() 通过取点、画图、计算,得到了
通过取点、画图、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
说明:补全表格时,相关数值保留一位小数.
(参考数据:![]() ) .
) .
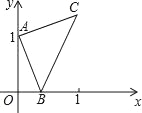
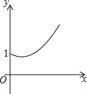
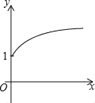
![]() 如图2,描出剩余的点,并用光滑的曲线画出该函数的图象.
如图2,描出剩余的点,并用光滑的曲线画出该函数的图象.
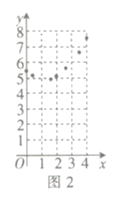
![]() 观察图象,下列结论正确的有 _ .
观察图象,下列结论正确的有 _ .
①函数有最小值,没有最大值
②函数有最小值,也有最大值
③当![]() 时,
时,![]() 随着
随着![]() 的增大而增大
的增大而增大
④当![]() 时,
时,![]() 随着
随着![]() 的增大而减小
的增大而减小