Question

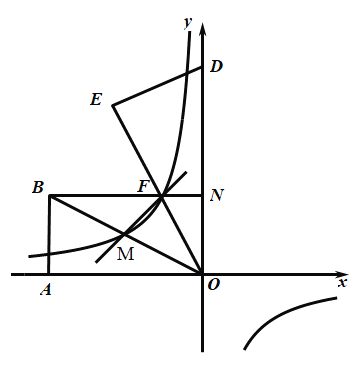
【题目】矩形的两条对称轴为坐标轴，点的坐标为.一张透明纸上画有一个点和一条抛物线，平移透明纸，使点与点重合，此时抛物线的函数表达式为，再次平移透明纸，使点与点重合，则该抛物线的函数表达式变为_______.

Answer 1

【答案】

【解析】

先由对称计算出C点的坐标，再根据平移规律求出新抛物线的解析式即可解题．

解：∵矩形ABCD的两条对称轴为坐标轴，
∴矩形ABCD关于坐标原点对称，
∵A点C点是对角线上的两个点，
∴A点、C点关于坐标原点对称，
∴C点坐标为（-2，-1）；
∴透明纸由A点平移至C点，抛物线向左平移了4个单位，向下平移了2个单位；
∵透明纸上点E与点A重合时，函数表达式为y=x2，
∴透明纸上点E与点C重合时，函数表达式为y=（x+4）2-2=x2+8x+14
故答案为：．