题目内容
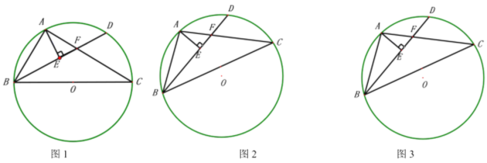
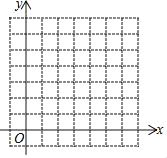
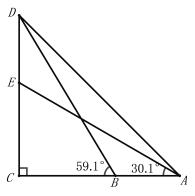
【题目】在![]() 中,
中,![]() ,
,![]() 、
、![]() 两点关于直线
两点关于直线![]() 对称,直线
对称,直线![]() 交
交![]() 于点
于点![]() ,交另一边于点
,交另一边于点![]() ,且
,且![]() ,则
,则![]() 的长为______.
的长为______.
【答案】64或![]() .
.
【解析】
分两种情况:①当点E在BC上时,作AF⊥BC于F,由勾股定理得出CE=25,由等腰三角形的性质得出BF=CF=![]() BC,然后证明△ACF∽△ECD得出
BC,然后证明△ACF∽△ECD得出![]() ,求出CF=32,即可得出结果;②当点E在AB上时,作BF⊥AC于F,由勾股定理得出AE=25,证明△ADE∽△AFB,得出
,求出CF=32,即可得出结果;②当点E在AB上时,作BF⊥AC于F,由勾股定理得出AE=25,证明△ADE∽△AFB,得出![]() ,求出BF=24,AF=32,得出CF=AC
,求出BF=24,AF=32,得出CF=AC![]() AF=8,由勾股定理求出BC即可.
AF=8,由勾股定理求出BC即可.
解:根据题意,∵![]() 、
、![]() 两点关于直线
两点关于直线![]() 对称,
对称,
∴直线L垂直平分AC,即DE⊥AC,
∵![]() ,
,
∴![]() ;
;
可分为两种情况进行
①当点E在BC上时,作AF⊥BC于F,如图:
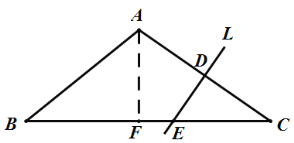
∵![]()
∴BF=CF=![]() BC,
BC,
在Rt△CDE中,由勾股定理,得
![]() ,
,
∵∠AFC=∠EDC=90°,∠C=∠C,
∴△ACF∽△ECD,
∴![]() ,即
,即![]() ,
,
∴CF=32,
∴BC=64;
②当点E在AB上时,作BF⊥AC于F,如图:

同理可求:AE=25,
∵∠A=∠A,∠ADE=∠AFB=90°,
∴△ADE∽△AFB,
∴![]() ,
,
即![]() ,
,
∴BF=24,AF=32,
∴CF=AC![]() AF=40
AF=40![]() 32=8,
32=8,
在Rt△CBF中,由勾股定理,得
![]() ;
;
∴![]() 的长为64或
的长为64或![]() ;
;
故答案为:64或![]() .
.

练习册系列答案
相关题目
【题目】疫情无情人有情,爱心捐款传真情.疫情期间,某企业员工积极参加献爱心活动,该企业率先捐款的50名员工的捐款情况统计如下表:
金额/元 | 50 | 100 | 200 | 500 | 100 |
人数 | 6 | 17 | 14 | 8 | 5 |
则他们捐款金额的平均数、中位数、众数分别是( )
A.276,100,200B.276,200,100C.370,100,100D.370,200,100