题目内容
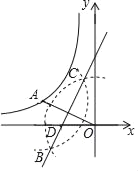
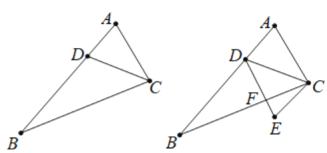
【题目】如图1,在△ABC中,D是AB上一点,已知AC=10,AC2=AD·AB.
(1)证明△ACD∽△ABC.
(2)如图2,过点C作CE∥AB,且CE=6,连结DE交BC于点F;
①若四边形ADEC是平行四边形,求![]() 的值;
的值;
②设AD=x,![]() =y,求y关于x的函数表达式.
=y,求y关于x的函数表达式.
【答案】(1)见解析;(2)①![]() ;②
;②![]()
【解析】
(1)由AC2=AD·AB得![]() ,再结合∠A=∠A即可得证;
,再结合∠A=∠A即可得证;
(2)①由平行四边形的性质可得AD=CE=6,DE∥AC,可证△BDF∽△BAC,可求解;
②通过△ACD∽△ABC,可得BC=![]() ,由平行线分线段成比例可得
,由平行线分线段成比例可得![]() ,代入可求解.
,代入可求解.
(1)证明:∵AC2=AD·AB,
∴![]() ,
,
又∵∠A=∠A,
∴△ACD∽△ABC;
(2)解:①∵四边形ADEC是平行四边形,
∴AD=CE=6,DE∥AC,
∵AC=10,AC2=ADAB,
∴AB=![]() ,
,
∵DE∥AC,
∴△BDF∽△BAC,
∴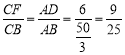 ;
;
②∵AC=10,AD=x,AC2=ADAB,
∴AB=![]() ,
,
∵△ACD∽△ABC,
∴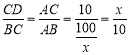 ,
,
∴BC=![]() ,
,
∵CE∥AB,
∴![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目