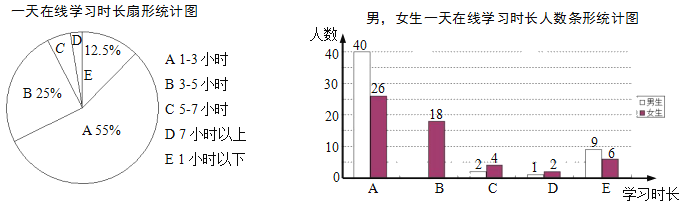
题目内容
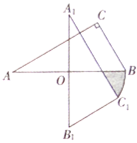
【题目】如图,点![]() 为
为![]() 的斜边
的斜边![]() 的中点,
的中点,![]() ,
,![]() ,以点
,以点![]() 为旋转中心顺时针旋转
为旋转中心顺时针旋转![]() 得到
得到![]() ,若
,若![]() ,当
,当![]() 时,图中弧
时,图中弧![]() 所构成的阴影部分面积为().
所构成的阴影部分面积为().
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
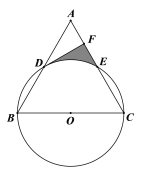
设A1C1与AB的交点为D,连接OC1,作DE⊥OC1于E,根据含30°角的直角三角形的性质,直角三角形斜边中线的性质以及平行线的性质求得∠BOC1=30°,OC1=2,DE=![]() ,然后根据扇形面积公式、三角形的面积公式即可求得阴影的面积.
,然后根据扇形面积公式、三角形的面积公式即可求得阴影的面积.
解:设A1C1与AB的交点为D,连接OC1,作DE⊥OC1于E,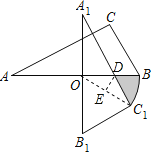
∵在△ABC中,∠C=90°,∠A=30°,BC=2,
∴AB=2BC=4,∠ABC=60°,
∵点O为Rt△ABC的斜边AB的中点,
∴OC=![]() AB=2,
AB=2,
∴OC1=OA1=2,
∴∠A1=∠A1C1O=30°,
∴∠A1OC1=120°,
∵BC∥A1C1,
∴∠ADA1=∠ABC=60°,
∵∠A1=∠A=30°,
∴∠A1OD=90°,
∴∠DOC1=30°,
∴∠DOC1=∠A1C1O,
∴OD=DC1,
∴OE=EC1=1,
∴DE=![]() OE=
OE=![]() ,
,
∴S阴影=S扇形-S△ODC1=![]() -
-![]() ×2×
×2×![]() =
=![]() π-
π-![]()
故选:A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目