Question

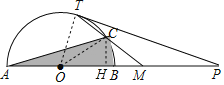
【题目】如图，半⊙O的半径为2，点P是⊙O直径AB延长线上的一点，PT切⊙O于点T，M是OP的中点，射线TM与半⊙O交于点C．若∠P=20°，则图中阴影部分的面积为（　　）

A. 1+ B. 1+ C. 2sin20°+ D.

Answer 1

【答案】A

【解析】

连接OT、OC，可求得∠COM=30°，作CH⊥AP，垂足为H，则CH=1，于是，S阴影=S△AOC+S扇形OCB，代入可得结论．

连接OT、OC，

∵PT切⊙O于点T，

∴∠OTP=90°，

∵∠P=20°，

∴∠POT=70°，

∵M是OP的中点，

∴TM=OM=PM，

∴∠MTO=∠POT=70°，

∵OT=OC，

∴∠MTO=∠OCT=70°，

∴∠OCT=180°-2×70°=40°，

∴∠COM=30°，

作CH⊥AP，垂足为H，则CH=OC=1，

S阴影=S△AOC+S扇形OCB=OACH+=1+，

故选A.