题目内容
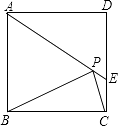
【题目】在△ABC中,∠BAC=120°,AD平分∠BAC,且AD=AB,若∠EDF=60°,其两边分别交边AB,AC于点E,F.
(1)求证:△ABD是等边三角形;
(2)求证:BE=AF.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连接BD,根据角平分线的性质可得∠BAD=60°,又因为AD=AB,即可证△ABD是等边三角形;(2)由△ABD是等边三角形,得出BD=AD,∠ABD=∠ADB=60°,证出∠BDE=∠ADF,由ASA证明△BDE≌△ADF,得出BE=AF.
(1)证明:连接BD,
∵∠BAC=120°,AD平分∠BAC
∴∠BAD=∠DAC=![]() ×120°=60°,
×120°=60°,
∵AD=AB,
∴△ABD是等边三角形;
(2)证明:∵△ABD是等边三角形,
∴∠ABD=∠ADB=60°,BD=AD,
∵∠DAC=![]() ∠BAC=60°,
∠BAC=60°,
∴∠DBE=∠DAF,
∵∠EDF=60°,
∴∠BDE=∠ADF,
在△BDE与△ADF中,
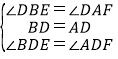 ,
,
∴△BDE≌△ADF(ASA),
∴BE=AF.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
【题目】小明到某超市购买A、B、C三种商品.其中A、B两种商品的单价之和正好等于C商品的单价,小明前两次购买商品的数量和总费用如下表:
商品A的数量 | 商品B的数量 | 商品C的数量 | 总费用(元) | |
第一次 | 2 | 3 | 2 | 230 |
第二次 | 1 | 4 | 3 | 290 |
(1)求A、B、C三种商品的单价;
(2)若小明第三次需要购置A、B、C三种商品共m个,其中C商品的数量是A商品的数量的2倍,恰好花了480元钱.
①求m的最大值;
②若小明在第三次购买A,B,C三种商品时正好遇上“买一送一”活动,即购买一个C商品即可赠送一个A商品或一个B商品(优先赠送A商品),求m的值.