题目内容
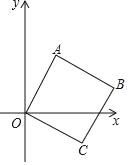
【题目】如图，将边长为2cm的正方形OABC放在平面直角坐标系中，O是原点，点A的横坐标为1，则点C的坐标为（ ）
A. （
，-1） B. （2，﹣1） C. （1，-） D. （﹣1，）
【答案】A
【解析】
作AD⊥y轴于D，作CE⊥y轴于E，则∠ADO=∠OEC=90°，得出∠1+∠2=90°，由正方形的性质得出OC=AO，∠1+∠3=90°，证出∠3=∠2，由AAS证明△OCE≌△AOD，得到OE=AD=1，CE=OD=
，即可得出结果．
作AD⊥y轴于D，作CE⊥y轴于E，如图所示：
则∠ADO=∠OEC=90°，∴∠1+∠2=90°．
∵AO=2，AD=1，∴OD=
，∴点A的坐标为（1，），∴AD=1，OD=．
∵四边形OABC是正方形，∴∠AOC=90°，OC=AO，∴∠1+∠3=90°，∴∠3=∠2．
在△OCE和△AOD中，∵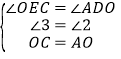
，∴△OCE≌△AOD（AAS），∴OE=AD=1，CE=OD=，∴点C的坐标为（，﹣1）．
故选A．
练习册系列答案
相关题目
【题目】已知关于x的代数式x2+bx+c，设代数式的值为y．下表中列出了当x分别取﹣1，0，1，2，3，4，5，…m，m+1…时对应的y值．
x | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | m | m+1 | |||
y | 10 | 5 | 2 | 1 | 2 | 5 | n | p | q |
（1）表中n的值为 ；
（2）当x＝ 时，y有最小值，最小值是 ；
（3）比较p与q的大小．