题目内容
如图,梯形ABCD中,AD∥BC,∠ABC=Rt∠,点E为AB上一点,且AE=BC=6,BE=AD=2,给出下列结论:
①梯形的面积等于32;
②CD的长为4
;
③△DEC为等腰直角三角形;
④DE平分∠ADC;
⑤∠BCD=60°.其中正确的个数有( )

①梯形的面积等于32;
②CD的长为4
| 5 |
③△DEC为等腰直角三角形;
④DE平分∠ADC;
⑤∠BCD=60°.其中正确的个数有( )
| A.2个 | B.3个 | C.4个 | D.5个 |

①由梯形的面积公式得s=
×AB=
×(6+2)=32,故正确;
②由D向BC作垂线,垂足为F,则DF=8,FC=6-2=4,故CD=
=4
,故正确;
③由△ADE≌△BEC得,DE=CE,∠AED=∠BCE,故∠AED+∠BEC=∠BCE+∠BEC=90°,
所以∠DEC=90°,△DEC为等腰直角三角形,故正确;
④取CD的中点G,连接GE,
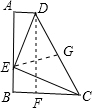
由③知,△DEC为等腰直角三角形,故GE=
CD=2
,且GE⊥CD,
而AE≠GE,不满足角平分线的性质,故DE平分∠ADC错误;
⑤在Rt△DFC中,tan∠BCD=
=
=2,故∠BCD≠60°,故错误.
综上,其中正确的个数有3个,故选B.
| AD+BC |
| 2 |
| 2+6 |
| 2 |
②由D向BC作垂线,垂足为F,则DF=8,FC=6-2=4,故CD=
| DE2+EC2 |
| 5 |
③由△ADE≌△BEC得,DE=CE,∠AED=∠BCE,故∠AED+∠BEC=∠BCE+∠BEC=90°,
所以∠DEC=90°,△DEC为等腰直角三角形,故正确;
④取CD的中点G,连接GE,

由③知,△DEC为等腰直角三角形,故GE=
| 1 |
| 2 |
| 5 |
而AE≠GE,不满足角平分线的性质,故DE平分∠ADC错误;
⑤在Rt△DFC中,tan∠BCD=
| DF |
| CF |
| 6+2 |
| 6-2 |
综上,其中正确的个数有3个,故选B.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目



 于AB,AC于点E,点F,下列结论正确的是( )
于AB,AC于点E,点F,下列结论正确的是( )

