题目内容
求证：等腰梯形下底的中点到两腰的距离相等．（要求完成图形，写出已知．求证，并加以证明）
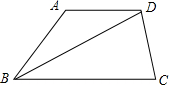
如图：四边形ABCD中，AD∥BC，AB=CD，E是BC的中点，过E作EF⊥AB于F，EG⊥CD于G，求证：EF=EG．
证明：∵E是BC中点，
∴BE=EC．
∵四边形ABCD是等腰梯形，
∴∠B=∠C．
∵∠BFE=∠CGE=90°，
∴△BFE≌△CGE．
∴EF=EG．
证明：∵E是BC中点，
∴BE=EC．
∵四边形ABCD是等腰梯形，
∴∠B=∠C．
∵∠BFE=∠CGE=90°，
∴△BFE≌△CGE．
∴EF=EG．
练习册系列答案
相关题目
一点到达端点时，另一点也随之停止运动．
从B、D同时出发，当其中一个点到达点A时，另一点也随之停止移动．设移动时间为t（s）．