Question

【题目】如图，在长方形ABCD中，把△BCD沿对角线BD折叠得到△BED，线段BE与AD相交于点P，若AB=2，BC=4．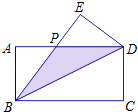

（1）BD=；
（2）点P到BD的距离是 ．

Answer 1

【答案】
（1） （或2 ）
（2） （或 ）
【解析】解：（1）∵四边形ABCD是长方形，
∴∠C=90°，
∴BD= = =2 ，
故答案为2 ；
2）在△APB与△DEP中，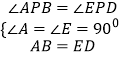
，
∴△APB≌△DEP，
∴AP=EP，
设AP=x，可知EP=x，PD=4﹣x，
∴在Rt△PED中，
x2+22=（4﹣x）2 ，
解得x= ．
即AP= ，
∴PD=4﹣ = ，
∴△BDP的面积= × ×2= ×2 点P到BD的距离，
∴点P到BD的距离= ，
故答案为 ．
（1）由勾股定理直接得出；（2）设AP=x，证出△ABP≌△EDP，可知EP=x，PD=8﹣x，根据翻折不变性，可知ED=DC=AB=2，然后在Rt△PED中，利用勾股定理求出x，再由三角形的面积即可求出结论．