题目内容
【题目】如图①,现有一张三角形ABC纸片,沿BC边上的高AE所在的直线翻折,使得点C与BC边上的点D重合.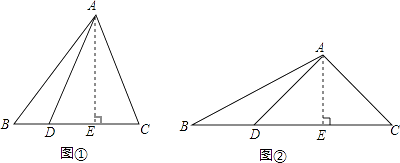
(1)填空:△ADC是三角形;
(2)若AB=15,AC=13,BC=14,求BC边上的高AE的长;
(3)如图②,若∠DAC=90°,试猜想:BC、BD、AE之间的数量关系,并加以证明.
【答案】
(1)等腰
(2)
解:设CE=x,则BE=14﹣x,
在Rt△AEC中,由勾股定理得:AE2=AC2﹣CE2,
∴AE2=132﹣x2
在Rt△ABE中,由勾股定理得:AE2=AB2﹣BE2,
∴AE2=152﹣(14﹣x)2
∴132﹣x2=152﹣(14﹣x)2
解得:x=5,
在Rt△AEC中,由勾股定理得: ![]()
(3)
解:猜想BC、BD、AE之间的数量关系为:BC﹣BD=2AE.
证明如下:
由(1)得:△ADC是等腰三角形,又∠DAC=90°,
∴△ADC是等腰直角三角形
又AE是CD边上的高,
∴DE=CE, ![]() ,
,
∴△AED与△AEC都是等腰直角三角形,
∴DE=AE=EC,即CD=2AE.
∵BC﹣BD=CD
∴BC﹣BD=2AE.
【解析】解:(1)∵三角形ABC纸片,沿BC边上的高AE所在的直线翻折,使得点C与BC边上的点D重合.
∴AD=AC,
∴△ADC是等腰三角形;
故答案为:等腰.
(1)根据折叠得到AD=AC,所以△ADC是等腰三角形;(2)设CE=x,利用勾股定理得到方程132﹣x2=152﹣(14﹣x)2解得:x=5,在Rt△AEC中,由勾股定理即可解答;(3)猜想BC、BD、AE之间的数量关系为:BC﹣BD=2AE.由△ADC是等腰三角形,又∠DAC=90°,得到△ADC是等腰直角三角形又AE是CD边上的高,所以△AED与△AEC都是等腰直角三角形,即可得到CD=2AE.由BC﹣BD=CD,即可解答.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案【题目】某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
交通方式 | 频数(人数) | 频率 |
公共汽车 | m | 0.25 |
小车 | 24 | 0.20 |
摩托车 | 36 | n |
自行车 | 18 | 0.15 |
其它 | 12 | 0.10 |
请根据图表信息解答下列问题:
(1)本次共抽样调查个学生;
(2)填空:频数分布表中的m= , n=;
(3)在扇形统计图中,请计算出“摩托车”所在的扇形的圆心角的度数.