题目内容
【题目】如图,在△ABC中,点E在BC上,CD⊥AB,EF⊥AB,垂足分别为D、F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数. 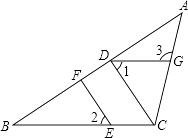
【答案】
(1)解:CD平行于EF,
理由是:∵CD⊥AB,EF⊥AB,
∴∠CDF=∠EFB=90°,
∴CD∥EF;
(2)解:∵CD∥EF,
∴∠2=∠DCB,
∵∠1=∠2,
∴∠1=∠DCB,
∴BC∥DG,
∴∠3=∠ACB,
∵∠3=115°,
∴∠ACB=115°.
【解析】(1)根据垂直定义求出∠CDF=∠EFB=90°,根据平行线的判定推出即可;(2)根据平行线的性质得出∠2=∠DCB,求出∠1=∠DCB,根据平行线的判定得出BC∥DG,根据平行线的性质得出∠3=∠ACB即可.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目