��Ŀ����
����Ŀ���ۺ��⡣
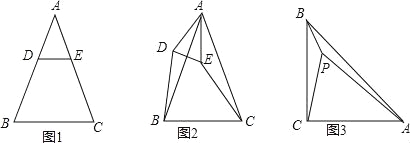
��1����ͼ�٣���ABC�У���D��E�ڱ�BC�ϣ�AEƽ�֡�BAC��AD��BC����C=40�㣬��B=60�㣬�١�CAE�Ķ������ڡ�DAE�Ķ�����
��2����ͼ�ڣ����ѣ�1���е�������AD��BC����ɡ�FΪAE�ӳ�����һ�㣬��FD��BC���������������䣬�����DFE�Ķ�����
��3���ڡ�ABC�У�AEƽ�֡�BAC����FΪEA�ӳ�����һ�㣬FD��BC���ҡ�C=������B=�£��£��������Բ����DFE�Ķ������æ����±�ʾ�������Լ�������Ӧͼ�β�˵�����ɣ� 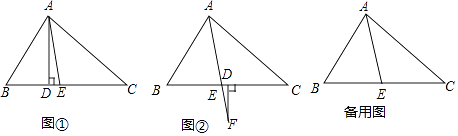
���𰸡�
��1���⣺��ͼ��1����
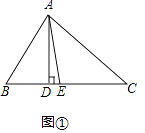
��AD��BC��
���ADB=90�㣬
���BAD=90�㩁��B=90�㩁60��=30�㣬
�ߡ�BAC=180�㩁��B����C=180�㩁60�㩁40��=80�㣬
��AEƽ�֡�BAC��
���BAE= ![]() ��BAC=
��BAC= ![]() ��80��=40�㣬
��80��=40�㣬
���DAE=��BAE����BAD=40�㩁30��=10�㣻
��2���⣺��ͼ2�У���AH��BC��H��
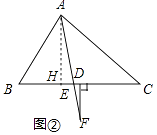
�ɣ�1����֪��HAE=10�㣬
��AH��EF��
���DFE=��HAE=10��
��3���⣺���ۣ���DFE= ![]() ����B����C�����������£�
����B����C�����������£�
��ͼ3�У���AH��BC��H��FD��BC��D��
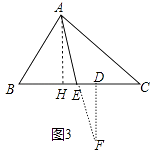
�ߡ�HAE=��EAB����BAH����BAH=90�㩁��B����BAE= ![]() ��180�㩁��B����C����
��180�㩁��B����C����
���HAE=90�㩁 ![]() ��B��
��B�� ![]() ��C����90�㩁��B��
��C����90�㩁��B��
= ![]() ����B����C����
����B����C����
��AH��FD��
���DFE=��HAE��
���DFE= ![]() ����B����C����
����B����C����
����������1����ͼ1�У������BAD����BAE�����ݡ�DAE=��BAE����BAD���ɽ�����⣮��2����ͼ2�У���AH��BC��H�����ã�1���н��ۣ���֤����DFE=��HAE���ɣ���3�����ۣ���DFE= ![]() ����B����C������ͼ3�У���AH��BC��H��FD��BC��D���ɡ�HAE=��EAB����BAH����BAH=90�㩁��B����BAE=
����B����C������ͼ3�У���AH��BC��H��FD��BC��D���ɡ�HAE=��EAB����BAH����BAH=90�㩁��B����BAE= ![]() ��180�㩁��B����C���Ƴ���HAE=90�㩁
��180�㩁��B����C���Ƴ���HAE=90�㩁 ![]() ��B��
��B�� ![]() ��C����90�㩁��B��=
��C����90�㩁��B��= ![]() ����B����C������AH��FD���Ƴ���DFE=��HAE�����ɽ�����⣮
����B����C������AH��FD���Ƴ���DFE=��HAE�����ɽ�����⣮
�����㾫����������Ŀ����֪���������������ε��ڽǺ���Ǻ������ε���ǵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�������һ������һ�ߵ��ӳ�����ɵĽǣ��������ε���ǣ������ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�