题目内容
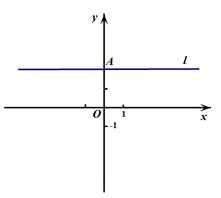
在平面直角坐标系xOy中,点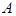 的坐标是
的坐标是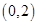 ,过点
,过点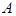 作直线
作直线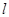 垂直
垂直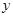 轴,点
轴,点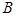 是直线
是直线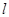 上异于点
上异于点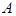 的一点,且
的一点,且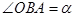 .过点
.过点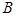 作直线
作直线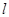 的垂线
的垂线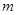 ,点
,点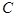 在直线
在直线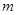 上,且在直线
上,且在直线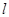 的下方,
的下方,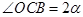 .设点
.设点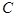 的坐标为
的坐标为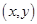 .
.
(1)判断△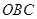 的形状,并加以证明;
的形状,并加以证明;
(2)直接写出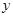 与
与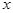 的函数关系式(不要求写自变量的取值范围);
的函数关系式(不要求写自变量的取值范围);
(3)延长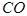 交(2)中所求函数的图象于点
交(2)中所求函数的图象于点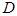 .求证:
.求证: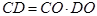 .
.
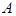 的坐标是
的坐标是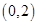 ,过点
,过点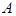 作直线
作直线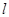 垂直
垂直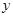 轴,点
轴,点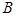 是直线
是直线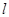 上异于点
上异于点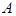 的一点,且
的一点,且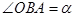 .过点
.过点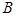 作直线
作直线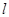 的垂线
的垂线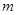 ,点
,点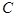 在直线
在直线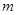 上,且在直线
上,且在直线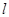 的下方,
的下方,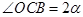 .设点
.设点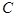 的坐标为
的坐标为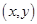 .
.
(1)判断△
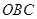 的形状,并加以证明;
的形状,并加以证明;(2)直接写出
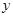 与
与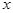 的函数关系式(不要求写自变量的取值范围);
的函数关系式(不要求写自变量的取值范围);(3)延长
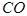 交(2)中所求函数的图象于点
交(2)中所求函数的图象于点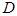 .求证:
.求证: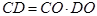 .
.(1)△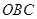 为等腰三角形;(2)
为等腰三角形;(2) ;
;
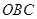 为等腰三角形;(2)
为等腰三角形;(2) ;
;试题分析:(1)由
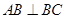 ,
,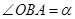 ,可得
,可得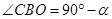 ,由
,由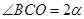 ,可得到
,可得到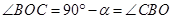 ,即可得到
,即可得到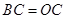 ,即可作出判断;
,即可作出判断;(2)根据等腰三角形的性质结合函数图象上的点的坐标的特征求解即可;
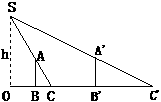
(3)过
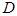 作
作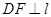 于
于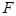 ,
,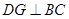 于
于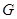 交直线
交直线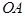 于
于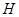 ,由BC=OC可得
,由BC=OC可得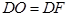 ,设
,设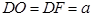 ,
,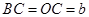 ,则
,则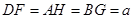 ,
,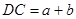 ,再分①当点
,再分①当点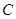 在
在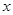 轴下方时,②当点
轴下方时,②当点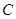 在
在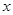 轴上方时,③当点
轴上方时,③当点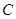 在
在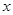 轴上时,三种情况,根据相似三角形的性质求解即可.
轴上时,三种情况,根据相似三角形的性质求解即可.(1)△
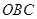 为等腰三角形
为等腰三角形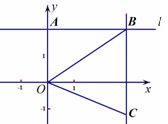
∵
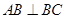 ,
,∴
 .
.∵
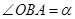 ,
,∴
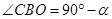 .
.∵
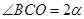 ,
,∴
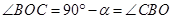 .
.∴
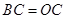 .
.∴△
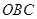 为等腰三角形;
为等腰三角形;(2)
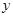 与
与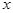 的函数关系式为
的函数关系式为 ;
;(3)过
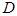 作
作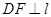 于
于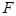 ,
,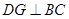 于
于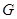 交直线
交直线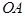 于
于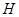 .
.∵C为抛物线上异于顶点的任意一点,且BC=OC,
∴
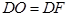 .
.设
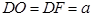 ,
,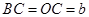 ,
,则
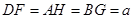 ,
,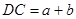 .
.①当点
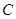 在
在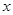 轴下方时,
轴下方时,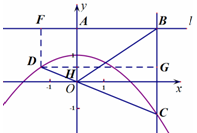
∵
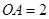
∴
 .
.∵
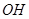 ∥
∥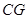 ,
,∴△
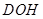 ∽△
∽△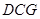 .
. ∴
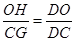 .
.∴
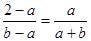
∴
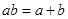 .
.∴
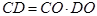 ;
;②当点
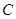 在
在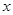 轴上方时,
轴上方时,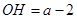 ,
,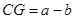 .同理可证
.同理可证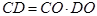 ;
;
③当点
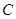 在
在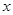 轴上时,
轴上时, .
.
∴
 .
.点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
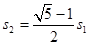 B.
B.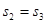 C.
C.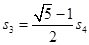 D.
D.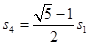
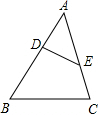
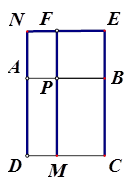
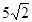 .且AB⊥BC,∠BCD=135°。点M是线段BC上的一个动点,连接AM、DM。
.且AB⊥BC,∠BCD=135°。点M是线段BC上的一个动点,连接AM、DM。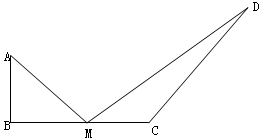
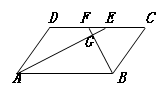
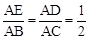 ,则
,则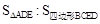 的值为
的值为