题目内容
【题目】如图,已知AB为半圆O的直径,P为半圆上的一个动点(不含端点),以OP、OB为一组邻边作POBQ,连接OQ、AP,设OQ、AP的中点分别为M、N,连接PM、ON.
(1)试判断四边形OMPN的形状,并说明理由.
(2)若点P从点B出发,以每秒15°的速度,绕点O在半圆上逆时针方向运动,设运动时间为ts.
①试求:当t为何值时,四边形OMPN的面积取得最大值?并判断此时直线PQ与半圆O的位置关系(需说明理由);
②是否存在这样的t,使得点Q落在半圆O内?若存在,请直接写出t的取值范围;若不存在,请说明理由.
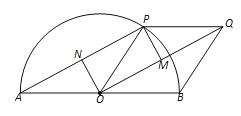
【答案】(1)四边形OMPN为矩形,理由见解析;(2)①当t=6秒时,四边形OMPN面积最大,此时,PQ与半圆O相切.理由见解析;②当8<t<12时,点Q在半圆O内.
【解析】
(1)先证四边形PQOA为平行四边形,再证四边形OMPN为平行四边形,根据等腰三角形三线合一,得ON⊥AP,进而即可得到结论;
(2)①由题意得S矩形OMPN=S△AOP,从而得△AOP的AO边上的高取得最大值,此时△AOP的面积取得最大值,进而即可得到t的值,根据切线的判定定理,即可得到结论;②考虑两个特殊情况:当点Q在半圆O上时,当点P与点A重合时,分别求出t的值,进而即可得到答案.
(1)四边形OMPN为矩形,理由如下:
∵四边形POBQ为平行四边形,
∴PQ∥OB,PQ=OB.
又∵OB=OA,
∴PQ=AO.
又∵PQ∥OA,
∴四边形PQOA为平行四边形,
∴PA∥QO,PA=QO.
又∵M、N分别为OQ、AP的中点,
∴OM=![]() OQ,PN=
OQ,PN=![]() AP,
AP,
∴OM=PN,
∴四边形OMPN为平行四边形.
∵OP=OA,N是AP的中点,
∴ON⊥AP,即∠ONP=90°,
∴四边形OMPN为矩形;
(2)①∵四边形OMPN为矩形,
∴S矩形OMPN=ON·NP=ON·![]() AP,即S矩形OMPN=S△AOP.
AP,即S矩形OMPN=S△AOP.
∵△AOP的底AO为定值,
∴当P旋转运动90°(运动至最高点)时,△AOP的AO边上的高取得最大值,此时△AOP的面积取得最大值,
∴t=90÷15=6秒,
∴当t=6秒时,四边形OMPN面积最大.
此时,PQ与半圆O相切.理由如下:
∵此时∠POB=90°,PQ//OB,
∴∠OPQ=90°,
∴PQ与半圆O相切;
②当点Q在半圆O上时,
∵四边形POBQ为平行四边形,且OB=OP,
∴四边形POBQ为菱形,
∴OB=BQ=OQ=OP=PQ,
∴∠POQ=∠BOQ=60°,即:∠BOP=120°,
∴此时,t=120°÷15°=8秒,
当点P与点A重合时,t=180°÷15°=12秒,
综上所述:当8<t<12时,点Q在半圆O内.



 导学教程高中新课标系列答案
导学教程高中新课标系列答案【题目】某中学初三年级积极推进走班制教学.为了了解一段时间以来,“至善班”的学习效 果,年级组织了多次定时测试,现随机选取甲、乙两个“至善班”,从中各抽取![]() 名同学在某一次定时测试中的数学成绩,其结果记录如下:
名同学在某一次定时测试中的数学成绩,其结果记录如下:
收集数据:
“至善班”甲班![]() 的名同学的数学成绩统计(满分为 100 分)(单位:分)
的名同学的数学成绩统计(满分为 100 分)(单位:分)
![]()
![]()
“至善班”乙班的![]() 名同学的数学成绩统计(满分为 100 分)(单位:分)
名同学的数学成绩统计(满分为 100 分)(单位:分)
![]()
![]()
整理数据:(成绩得分用![]() 表示)
表示)
分数 数量 班级 |
|
|
|
|
|
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据,并回答下列问题:
![]() 完成下表:
完成下表:
平均数 | 中位数 | 众数 | |
甲班 |
|
|
|
乙班 |
|
|
|
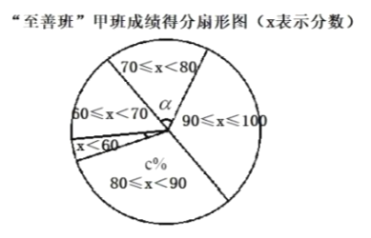
![]() 在“至善班”甲班的扇形图中, 成绩在
在“至善班”甲班的扇形图中, 成绩在![]() 的扇形中,所对的圆心角
的扇形中,所对的圆心角![]() 的度数为 . 估计全部“至善班”的
的度数为 . 估计全部“至善班”的![]() 人中优秀人数为 人.(
人中优秀人数为 人.(![]() 分及以上为优秀).
分及以上为优秀).
![]() 根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本 的同学的学习效果更好一些,你所做判断的理由是:
根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本 的同学的学习效果更好一些,你所做判断的理由是:
①
②