��Ŀ����
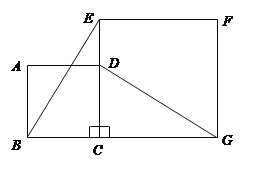
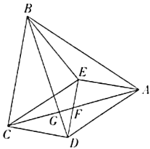
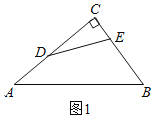
����Ŀ����ͼ1��Rt��ABC�У���D��E�ֱ�Ϊֱ�DZ�AC��BC�ϵĵ㣬������AD2+BE2��DE2�����DEΪR��ABC���������ָ���������Ȼ����DEΪ��ABC����λ��ʱ��DE�ǡ�ABC��һ�������ָ��ߣ�
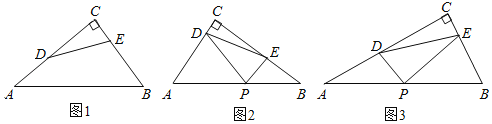
��1����ͼ1��AB��10��cosA��![]() ��AD��3����DEΪ�����ָ��ߣ���BE�ij����� ����
��AD��3����DEΪ�����ָ��ߣ���BE�ij����� ����
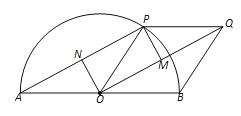
��2����ͼ2����AC���ϵĵ�D����Rt��ABC�е�б��AB��ȡ��P��ʹ��DP��DA������P��PE��PD��BC�ڵ�E������DE����֤��DE��ֱ�ǡ�ABC�������ָ��ߣ�
��3����ͼ3����Rt��ABC�У�AC��10��BC��5��DE���������ָ��ߣ���P��б��AB���е㣬����PD��PE����cos��PDE��ֵ��
���𰸡���1��![]() ����2�������������3��
����2�������������3��![]()
��������
��1�������������BC�ij�����BE��x����CE��6��x���ɹ��ɶ�����DE2��CD2+CE2��52+��6��x��2�����뵽AD2+BE2��DE2�м������BE��
��2���ָ��������ҳ�EP=EB�����ɹ��ɶ����ó�DP2+EP2��DE2=AD2+BE2��DE��ֱ�ǡ�ABC�������ָ��ߣ�
��3���������������ߣ��ӳ�DP��F��ʹPF��PD������BF��EF����������ó�ED��EF��
�ٹ���P��PM��AC��PN��BC��֤����MPD�ס�NPE����PD��a����PE��2a�����DE���������cos��PDE��ֵ��
�⣺��1����AB��10��cosA��![]() ��
��
��cosA��![]() ��
��
��AC��8��CD��5��
��BC=![]() ��
��![]() ��6��
��6��
��BE��x����CE��6��x��
��Rt��CDE��DE2��CD2+CE2��52+��6��x��2��
��DEΪ�����ָ��ߣ�
��AD2+BE2��DE2��
��32+x2��52+��6��x��2��
��ã�x��![]() ��
��
��BE��![]() ��
��
�ʴ�Ϊ��![]() ��
��
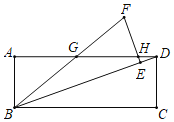
��2��֤������ͼ2��

��DA��DP��
���DAP����DPA��
��PE��PD��
���DPA+��EPB��90����
�֡�A����B��
���EPB����B��
��EP��EB��
��AD2+BE2��DP2+EP2��DE2��
��DE��ֱ�ǡ�ABC�������ָ��ߣ�
��3���⣺�ӳ�DP��F��ʹPF��PD������BF��EF��
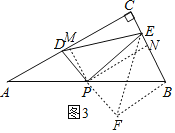
��AP��BP����APD����BPF��
���APD�ա�BPF��SAS����
��AD��BF����A����FBP��
���EBF����CBA+��FBP����CBA+��A��90����
��DE�������ָ��ߣ�
��DE2��AD2+BE2��BF2+BE2��EF2����ED��EF��
��PD��PF��
���EPD��90����
����P��PM��AC��PN��BC��
���MPD����NPE��90������MPE��
���MPD�ס�NPE��
��![]() ��
��
��PD��a����PE��2a����DE��![]() ��
��![]() a��
a��
��cos��PDE��![]() ��
��![]() ��
��