题目内容
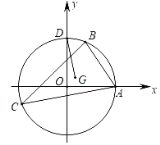
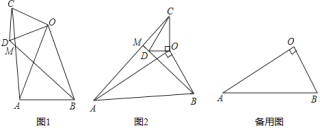
【题目】(1)问题发现:如图(1),在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=36°,连接AC,BD交于点M.①![]() 的值为 ;②∠AMB的度数为 ;
的值为 ;②∠AMB的度数为 ;
(2)类比探究 :如图(2),在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC,交BD的延长线于点M.请计算![]() 的值及∠AMB的度数.
的值及∠AMB的度数.
(3)拓展延伸:在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M.若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
【答案】(1)①1;②36°;(2)![]() =
=![]() ,∠AMB=90°;(3)3
,∠AMB=90°;(3)3![]() 或4
或4![]() .
.
【解析】
(1)①由∠AOB=∠COD推出∠COA=∠DOB,利用边角边即可证△COA与△DOB全等,即可求出结果;
②先证出∠CAO与∠DBO相等,分别加∠AOB,∠AMB,结果仍相等,即可得到∠AOB=∠AMB=36°;
(2)证明△DOB与△COA相似即可求出AC:BD的值,再通过对顶角相等及∠OBD=∠CAO即可证出∠AMB的度数为90°;
(3)分点M在直线OA的左侧和右侧两种情况讨论,利用相似三角形对应边的比设未知数,在Rt△AMB中利用勾股定理构造方程即可求出AC的长.
解:(1)①∵∠AOB=∠COD=36°,
∴∠AOB+∠DOA=∠COD+∠DOA,
∴∠COA=∠DOB,
又∵OA=OB,OC=OD,
∴△COA≌△DOB(SAS),
∴AC=BD,
∴![]() =1,
=1,
故答案为:1;
②设AO与BD交于点E,
由①知,△COA≌△DOB,
∴∠CAO=∠DBO,
∵∠AOB+∠DBO=∠DEO,
∠AMB+∠CAO=∠DEO,
∴∠AOB=∠AMB=36°,
故答案为:36°;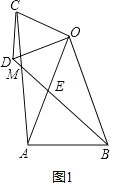
(2)在△OAB和△OCD中,
∵∠AOB=∠COD=90°,∠OAB=∠OCD=30°,
∴tan30°=![]() ,
,
∵∠AOB+∠DOA=∠COD+∠DOA,
即∠DOB=∠COA,
∴△DOB∽△COA,
∴![]() ,
,
∠DBO=∠CAO,
∵∠DBO+∠OEB=90°,∠OEB=∠MEA,
∴∠CAO+∠MEA=90°,
∴∠AMB=90°,
∴![]() =
=![]() ,∠AMB=90°;
,∠AMB=90°;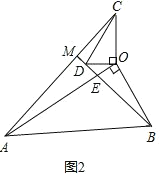
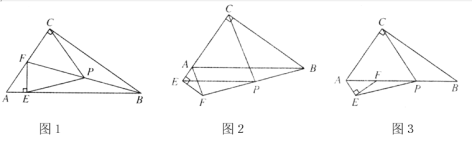
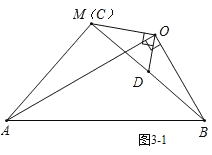
(3)①如图3-1,当点M在直线OB左侧时,
在Rt△OCD中,∠OCD=30°,OD=1,
∴CD=2,
在Rt△OAB中,∠OAB=30°,OB=![]() ,
,
∴AB=2![]() ,
,
由(2)知,∠AMB=90°,且![]() =
=![]() ,
,
∴设BD=x,则AC=AM=![]() x,
x,
在Rt△AMB中,
AM2+MB2=AB2,
∴(![]() x)2+(x+2)2=(2
x)2+(x+2)2=(2![]() )2,
)2,
解得,x1=3,x2=-4(舍去),
∴AC=AM=3![]() ;
;
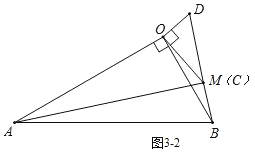
②如图3-2,当点M在直线OB右侧时,
在Rt△AMB中,
AM2+MB2=AB2,
∴(![]() x)2+(x-2)2=(2
x)2+(x-2)2=(2![]() )2,
)2,
解得,x1=4,x2=-3(舍去),
∴AC=AM=4![]() ,
,
综上所述,AC的长为3![]() 或4
或4![]() .
.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案